Expected Value Formula

Formula to Calculate Expected Value

Expected value formula is used in order to calculate the average long-run value of the random variables available and according to the formula the probability of all the random values is multiplied by the respective probable random value and all the resultants are added together to derive the expected value.

Mathematically, the expected value equation is represented as below,

where

• p_i = Probability of random value
• a_i = Probable random value

Expected Value Calculation (Step by Step)

The calculation of the expected value of a series of random values, we can derive by using the following steps:

• Step 1: Firstly, determine the different probable values. For instance, different probable asset returns can be a good example of such random values. The probable values are denoted by a_i.
• Step 2: Next, determine the probability of each of the values mentioned above, denoted by p_i. Each probability can be any number in the range of 0 to 1 such that the total of the probabilities is equal to one, i.e., 0 ≤ p₁, p₂,…., p_n ≤ 1 and p₁ + p₂ +….+ p_n = 1.
• Step 3: Finally, we calculate the expected value of all different probable values, as the sum product of each probable value and corresponding probability as below,

Expected value = p₁ * a₁ + p₂ * a₂ + ………… + p_n * a_n

Examples

Example #1

Let us take an example of Ben, who has invested in two securities within his investment portfolio. The probable rate of return of both the securities (security P and Q) are as given below. Based on the given information, help Ben to decide which security is expected to give him higher returns.

We will use the following data for the calculation of the expected value.

In this case, the expected value is the expected return of each security.

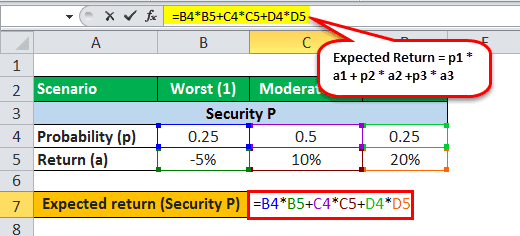
Expected Return of Security P

The expected return of security P can be calculated as,

• Expected return (P) = p₁ (P) * a₁ (P) + p₂ (P) * a₂ (P) + p₃ (P) * a₃ (P)
• = 0.25 * (-5%) + 0.50 * 10% + 0.25 * 20%

Therefore, the calculation of Expected return is as follows,

• Expected return = 8.75%

Expected Return of Security Q

The expected return of security Q can be calculated as,

• Expected return (Q) = p₁ (Q) * a₁ (Q) + p₂ (Q) * a₂ (Q) + p₃ (Q) * a₃ (Q)
• = 0.35 * (-2%) + 0.35 * 12% + 0.30 * 18%

Therefore, the calculation of Expected return is as follows,

• Expected Return= 8.90%

Therefore, for Ben security Q is expected to give higher returns than that of security P.

Example #2

Let us take another example where John is to assess the feasibility of two upcoming development projects (Project X and Y) and choose the most favorable one. According to estimates, Project X is expected to achieve a value of $3.5 million with a probability of 0.3 and achieve a value of $1.0 million with a probability of 0.7. On the other hand, Project Y is expected to achieve a value of $2.5 million, with a probability of 0.4 and achieve a value of $1.5 million, with a probability of 0.6. Determine for John which project is expected to have a higher value on completion.

We will use the following data for the calculation of the expected value.

Expected Value of Project X

The calculation of the expected value of Project X can be done as follows,

• Expected Value (X) = 0.3 * $3,500,000 + 0.7 * $1,000,000

Calculation of Expected Value of Project X will be –

• Expected Value (X) = $1,750,000

Expected Value of Project Y

The calculation of the expected value of Project Y can be done as follows,

• Expected Value (Y)= 0.4 * $2,500,000 + 0.6 * $1,500,000

Calculation of Expected Value of Project Y will be –

• Expected Value = $1,900,000

Therefore, on completion Project Y is expected to have a higher value than that of Project X.

Relevance and Use

An analyst needs to understand the concept of expected value as it is used by most investors to anticipate the long-run return of different financial assets. The expected value is commonly used to indicate the anticipated value of an investment in the future. Based on the probabilities of possible scenarios, the analyst can figure out the expected value of the probable values. Although the concept of expected value is often used in various multivariate models and scenario analysis, it is predominantly used in the calculation of expected return.

Recommended Articles

This article has been a guide to the Expected Value Formula. Here we learn how to calculate the expected value along with examples and a downloadable excel template. You can know more about financial analysis from the following articles –

• Value Formula in Excel
• Binomial Distribution Formula
• Median Formula
• Formula of Present Value