Elastic Net

Published on :

21 Aug, 2024

Blog Author :

Edited by :

Reviewed by :

Elastic net (also called ELNET) regression is a statistical hybrid method that combines two of the most often used regularized linear regression techniques, lasso, and ridge, to deal with multicollinearity issues when they arise between predictor variables. Regularization aids in solving the overfitting issues with the models.

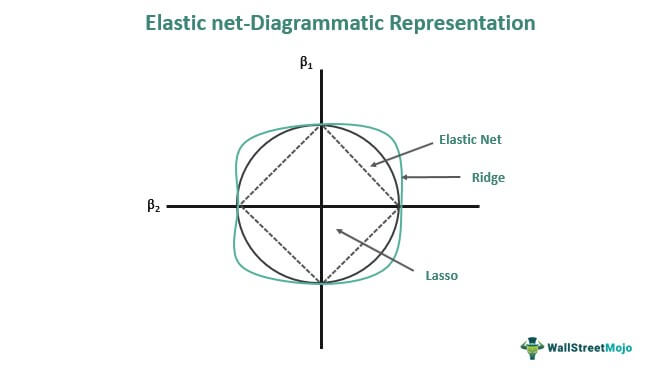
It is also used for regularizing and choosing the essential predictor variables that significantly impact the response variable. Ridge employs an L2 penalty, while lasso employs an L1. Since the elastic net utilizes both the L2 and the L1 models, the question of choosing between either one does not arise.

What Is Elastic Net

Elastic net is a combination of two of the best shrinkage regression approaches. They are Ridge regression (L2 penalty), which deals with high-multicollinearity problems, and LASSO regression (L1 penalty), which deals with feature selection of regression coefficients.
ELNET uses coefficient regression shrinkage towards zero or equal to zero to reduce the occurrence of predictor variables.
The primary idea underlying the elastic net is regularization. Regularization is considered in situations where the model is overfitting. It is a solution for reducing errors by properly fitting a function to the training dataset.

Elastic Net Explained

Elastic net is a regression technique that simultaneously applies regularization and variable selection. The primary idea underlying the elastic net is regularization. Regularization is considered in situations where the model is overfitting. Overfitting is a problem that arises when the model gives results on the training dataset but produces errors on the test dataset. Regularization is a solution for reducing errors by properly fitting a function to the training dataset. These functions are also otherwise known as elastic net penalties.

The elastic net penalty comes in two varieties: l1 and l2. The lasso and ridge regression models are two types of regularization models that apply l1 and l2 penalties, respectively. The absolute value of the coefficient's magnitude is added as a penalty term in the lasso regression model. The ridge regression adds the coefficient's squared magnitude as a penalty to the loss function.

Thus, it deals with both multicollinearity problems and the selection of regression coefficients. ELNET uses coefficient regression shrinkage towards zero or equal to zero to reduce the occurrence of predictor variables. The tuning parameter (λ1) multiplied by the sum of coefficient variables (l1 norms) absolute values is utilized for this purpose. The tuning parameter (λ2) is multiplied by the l2 norm's squared coefficient variables to handle the high correlation between the predictor variables. The ELNET regression approach helps produce a fitting, interpretable model by minimizing unnecessary variables that do not appear in the final model to improve prediction accuracy. The ELNET manages multicollinearity by maintaining or excluding highly correlated predictor variables from the fitted model.

Formula

An elastic net is a combination of two regressions, lasso, and ridge, and hence the resultant equation to calculate it is:

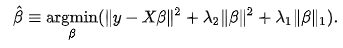
Examples

Check out these examples to get a better idea:

Example #1

A study gathered the Social Vulnerability Index (SVI) and Democratic vote percentage to determine which county-level sociodemographic parameters significantly correlated with the COVID-19 case rate. ELNET regression was used for the study to deal with issues of model overfitting and variable collinearity. Statistically speaking, it resulted in improved predictions compared to the results of multiple regressions.

Example #2

ELNET and lasso regressions were compared for major element analysis of the rocks and soil using laser-induced breakdown spectroscopy (LIBS). It was intended to be used by "Curiosity," the Mars Science Laboratory rover, to analyze soil and rock.

It was found that the RMSEP (root mean squared errors of prediction) value was lower for seven of the ten main elemental oxide compositions when using the ELNET model. For each of the ten major elemental oxides, the ELNET model had more non-zero coefficient values than the lasso. This results from the elastic net penalty's ability to average. While both methods proved reliable, ELNET projected a more stable model compared to the lasso model.

Elastic Net vs Ridge vs Lasso

Some differences between the three are given as follows:

#1 - Handling Bias

The weights of unnecessary features are typically reduced to zero by lasso and elastic nets. However, ridge regression should be the initial option if there are few features that all appear significant in relation to the target because it frequently produces small but evenly distributed weights. When there are more characteristics or features than training examples or when several characteristics are highly correlated, the elastic net is favored over lasso regression because, in these situations, the lasso can introduce some bias.

Therefore, the elastic net handles bias better than ridge and lasso regression. Small bias disturbs prediction because it depends on a variable. Elastic net hence handles collinearity better than ridge and lasso regression combined.

#2 - Handling Complexity

Elastic net regression outperforms ridge and lasso regression in complexity, as neither method considerably reduces the number of variables. Here, the inability to reduce variables results in a decline in the model's accuracy.

#3 - Handling Accuracy

Since lasso regression predictors don't perform as accurately as ridge and elastic net, they could be considered superior to the lasso regression. Lasso regression frequently chooses non-zero as predictors, which can occasionally reduce accuracy when relevant predictors are considered non-zero.

Frequently Asked Questions (FAQs)

1. When to use elastic net regression?

An elastic net regression is appropriate when the variables form groups containing highly correlated independent variables. These selections are incorporated into the model development procedure to raise its accuracy. It is good as it maintains the selection quality of the lasso penalty as well as the effectiveness of the ridge penalty.

2. Why do we need elastic net regularization?

The method improves the sampling process by facilitating the correlation-based identification of the variables and increasing the number of variables selected. It also balances the two penalties, leading to greater performance than models with just one penalty for particular problems.

3. Is elastic net better than lasso?

The ELNET method comes with a solution for the lasso approach's drawbacks—namely, it only records a few sample values for high-dimensional data. The inclusion of "n" numbers of variables up until saturation is possible with the elastic net approach.