Table Of Contents
Duration Formula Meaning
The duration formula is a measure of a bond’s sensitivity to changes in the interest rate, and it is calculated by dividing the sum product of discounted future cash inflow of the bond and a corresponding number of years by a sum of the discounted future cash inflow. A bond’s duration and coupon rate are factors that affect the duration.
The cash inflow basically comprises coupon payments and the maturity at the end. It is also known as Macaulay duration. Macaulay duration is used to find out the total time it might take for an investor to recover the full amount from the cashflows as an addition to the bond duration formula.
Duration Formula Explained
The duration formula is used to determine a bond and a fixed-income portfolio’s sensitivity toward interest rate changes. Typically, when the interest rates of a bond rise, the higher the duration to maturity, the higher the chances of its price falling.
The two factors that can have a major effect on the duration of a bond are the coupon rate and the time left for maturity. Usually, the Macaulay duration measures the total time it might take for an investor to recover the bond price through all related cash flows.
The changes in the price of a bond by 1% and the changes in interest rates due to that are calculated by the effective duration formula. A fixed income portfolio’s effective duration formula is derived by using the weighted average method individually for each bond.
The most common methods to calculate the duration of a bond are the Macaulay method and the modified duration method. By understanding this factor of fixed-income investment, investors can gain clarity on two factors relating to risk- credit risk and interest rate risk.
Both these factors have an effect on the yield on the maturity of the bond. In the case of a zero-coupon bond, the duration and time to maturity are equal since this type of bond does not pay coupons.
Formula
Let us understand the bond duration formula which can act as a basis for our understanding of this concept in detail and its related factors through the explanation below.
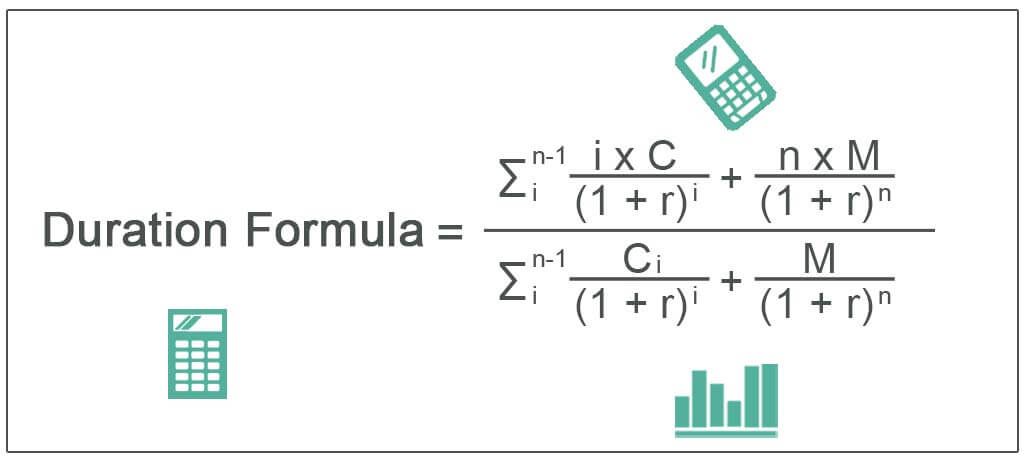
Duration Formula = /
where,
- C = Coupon payment per period
- M= Face or Par value
- r =Effective periodic rate of interest
- n = Number of periods to maturity
Further, the denominator, which is the summation of the discounted cash inflow of the bond, is equivalent to the present value or price of the bond. Therefore, the formula for the duration can be further simplified as below,

Explanation
The equation for the duration can be computed by using the following steps:
Firstly, the face or par value of the bond issuance is figured out, and it is denoted by M.
Now, the coupon payment of the bond is calculated based on the effective periodic rate of the interest. Then the frequency of the coupon payment is also determined. The coupon payment is denoted by C, and the effective periodic rate of interest is denoted by r.
Now, the total number of periods till maturity is computed by multiplying the number of years till maturity and the frequency of the coupon payments in a year. The number of periods till maturity is denoted by n. Also, the time of the periodic payment is noted, which is denoted by i.
Finally, based on the available information, the equation for the duration can be derived as below,

Examples
Let's see some simple to advanced types of duration formula to give us a practical understanding of effective duration formula and its related factors.
Example #1
Let us take an example of a bond with annual coupon payments. Let us assume that company XYZ Ltd has issued a bond having a face value of $100,000, carrying an annual coupon rate of 7% and maturing in 5 years. The prevailing market rate of interest is 10%.
Given, M = $100,000
- C = 7% * $100,000 = $7,000
- n = 5
- r = 10%
The denominator or the price of the bond is calculated using the formula as,

- Bond price = 84,281.19
Calculation of the numerator of Duration formula is as follows -

= (6,363.64 + 11,570.25 + 15,777.61 + 19,124.38 + 310,460.70)
= 363,296.50
Therefore, the calculation of duration of the bond will be as below,

Duration = 363,296.50 / 84,281.19
- Duration =4.31 years
Example #2
Let us take an example of a bond with annual coupon payments. Let us assume that company XYZ Ltd has issued a bond having face value of $100,000 and maturing in 4 years. The prevailing market rate of interest is 10%. Calculate the bond duration for the following annual coupon rate: (a) 8% (b) 6% (c) 4%
Given, M = $100,000
- n = 4
- r = 10%
Calculation for Coupon Rate of 8%
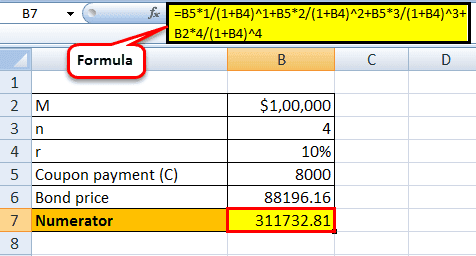
Coupon payment (C)= 8% * $100,000 = $8,000
The denominator or the price of the bond is calculated using the formula as,

- Bond price = 88,196.16
Calculation of the numerator of the Duration formula will be as follows -

= 311,732.81
Therefore, the calculation of duration of the bond will be as below,

Duration = 311,732.81/ 88,196.16
- Duration = 3.53 years
Calculation for Coupon Rate of 6%
Coupon payment (C) = 6% * $100,000 = $6,000
The denominator or the price of the bond is calculated using the formula as,

- Bond price = 83,222.46
Calculation of the numerator of the Duration formula will be as follows -

= 302,100.95
Therefore, the calculation of the duration of the bond will be as below,

Duration = 302,100.95 / 83,222.46
- Duration = 63 years
The calculation for Coupon Rate of 4%
Coupon payment = 4% * $100,000 = $4,000
The denominator or the price of the bond is calculated using the formula as,

- Bond price = 78,248.75
Calculation of the numerator of the Duration formula will be as follows -

= 292,469.09
Therefore, the calculation of the duration of the bond will be as below,

Duration Formula = 292,469.09 / 78,248.75
- Duration = 3.74 years
From the example, it can be seen that the duration of a bond increases with the decrease in coupon rate.
Relevance and Use
It is important to understand the concept of the bond duration formula as it is used by bond investors to check its sensitivity to changes in interest rates. The duration of a bond basically indicates how much the market price of a bond will change owing to the change in the rate of interest. It is noteworthy to remember that rate of interest and bond price move in opposite directions, and as such, bond price rise when the rate of interest falls and vice versa.
In case investors are seeking benefits from a fall in interest rate, the investors will intend to buy bonds with a longer duration, which is possible in the case of bonds with lower coupon payments and long maturity. On the other hand, investors who want to avoid the volatility in interest rates, the investors will be required to invest in bonds that have a lower duration or short maturity and higher coupon payment.