Table Of Contents
What is Discount Rate?
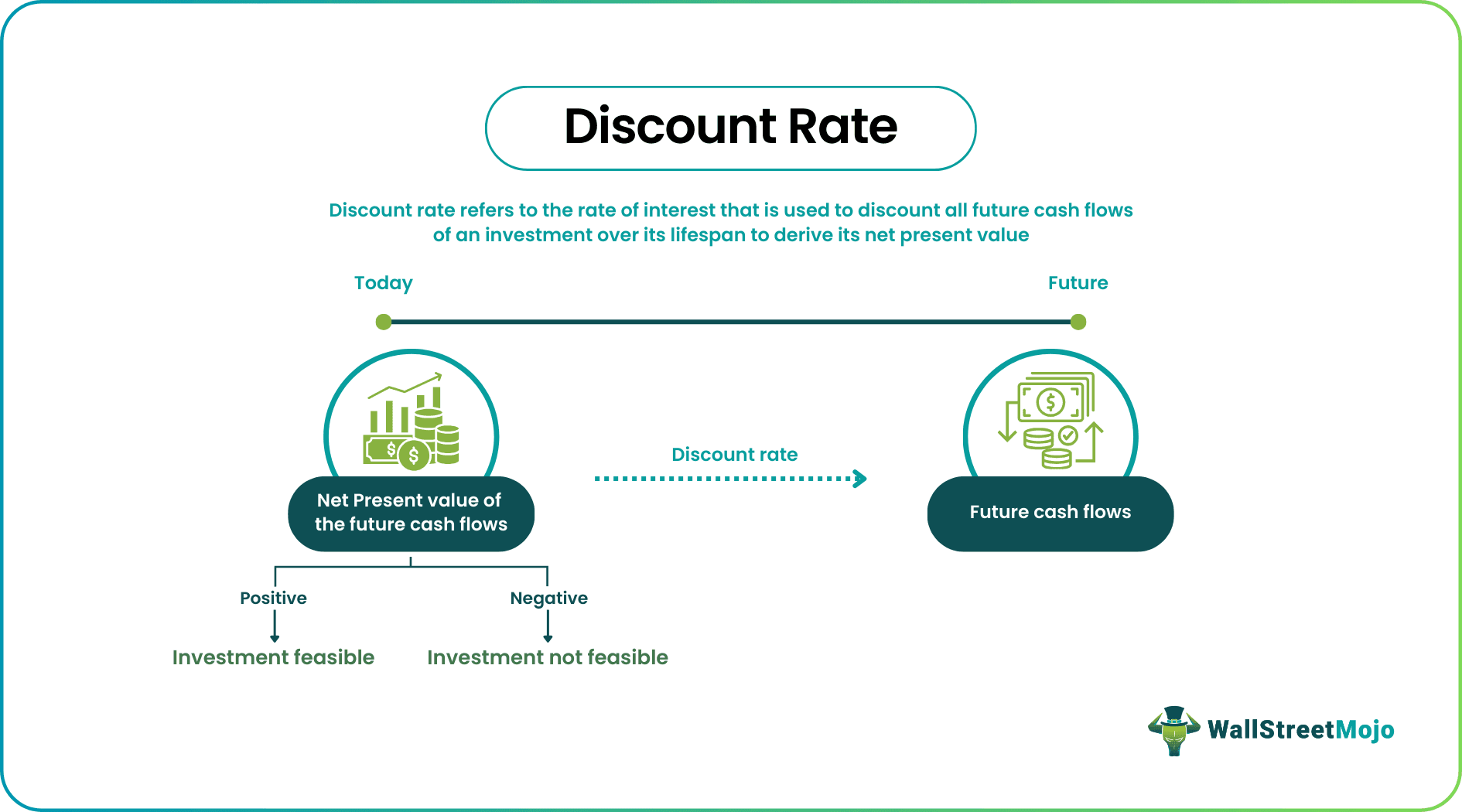
The discount rate refers to the rate of interest that is applied to future cash flows of an investment to calculate its present value. It is the rate of return that companies or investors expect on their investment. An investment’s net present value computed through discounting reveals its viability.
It is often the expected rate of return from an investment or the Weighted Average Cost of Capital (WACC). Discounting future cash flows is essential as the future money is less valuable than current money as per the concept of the time value of money. Therefore, discounting helps to understand the real value of future money today.
Key Takeaways
- Discount rate refers to the rate of interest that is used to discount all future cash flows of an investment to derive its Net Present Value (NPV).
- NPV helps to determine an investment or project’s feasibility.
- If NPV is a positive value, the investment is viable; otherwise not.
- WACC, Cost of Equity, Cost of Debt, Hurdle Rate, and Risk-free Rate are the types of discount rates applicable.
Discount Rate Explained
Discount rate is the interest rate used to find the net present value (NPV) of a project’s future cash flows. NPV helps to determine the profitability of an investment or project. Therefore, this interest rate determines whether a project is viable or not.
Each company or investor expects certain future cash flows when taking up a project or investment. However, these future cash flows can’t be considered as such to determine the feasibility of the project. This is because the value of money decreases with time. Also, there is uncertainty or risk related to the future, which must be taken into account.
Thus, companies conduct a discounted cash flow (DCF) analysis. DCF analysis uses discounting to calculate the project’s value today based on its future cash flows. In other words, it lets investors determine the project’s NPV.
A positive NPV indicates that the present value of cash flows is greater than the initial cost of the investment, i.e., returns exceed the costs. This means that if the NPV is positive, the project is worthwhile; otherwise, it is not. Thus, investing in such scenarios is a wise decision.
Note that NPV and discount rate have an inverse relationship. The higher the rate, the lower the NPV and vice versa. This is because the future cash flows reduce in value if discounted at a higher rate. Therefore, a lower rate is always desirable.
Discount Rate Types
The future value of an investment doesn’t amount to anything for companies. They can judge the utility of the investment only on the basis of its value today. So discount rate comes in handy to compute the present value of any project or investment.
The companies opt for different rates. For instance, some use the rate of return they wish to receive from the investments depending on the risk involved, while others use their weighted average cost of capital (WACC) as a discount rate.
Therefore, different types of rates apply to the investments based on the nature and the purpose for which they are being used.
- WACC: It is the required rate of return that a company’s investors expect in return for capital. It comes in handy to compute the equity value of a company.
- Cost of Equity: It is the rate of return that a company pays to its equity shareholders. It is used to compute the equity value of a company.
- Cost of Debt: It is the rate of interest that a company pays to its bondholders. The valuation of fixed-income assets uses it.
- Hurdle Rate: It is the minimum acceptable rate of return for investing in a project. It evaluates investments in internal corporate projects.
- Risk-free Rate: It is the rate of return on an investment with no associated risks. It helps assess the time value of money.
Formula for Discount Rate
To calculate NPV, this is how the discount rate is used:
Where,
- F = projected cash flow of the year
- R = discount rate
- n = number of years of cash flow in future
Calculation & Examples
Suppose a company makes an initial investment of $2,000, which is likely to yield cash inflows of $1000 per year for four years. The total future cash inflow, in this case, would be $4,000. If the rate is 10%, then the present value calculations are as follows:
| Particulars | Year 0 | Year 1 | Year 2 | Year 3 | Year 4 |
|---|---|---|---|---|---|
| Cash flows | ($2000) | $1000 | $1000 | $1000 | $1000 |
| Present value of cash flows | ($2000) | $909 | $826 | $751 | $683 |
Year 1
= $909
Year 2
= $826
Year 3
= $751
Year 4
= $683
Total present value = PV for Year 1 + PV for Year 2 + PV for Year 3 + PV for Year 4
= 909+826+751+683
= $3,169
The initial investment needs to be subtracted from the sum of the present value to determine whether making this investment is profitable or not.
NPV = Total Present Value – Initial Investment
= 3169 – 2000
= 1,169
As the NPV value is positive, the investment is fruitful.
Issues
Though discount rate helps investors find out a project's NPV and make major investment decisions, there are a few issues that users need to take care of:
- Since future cash flows are uncertain, the NPV calculations using discount rate is, at best, guesswork, which may or may not work.
- The discount rate remains the same throughout the years of activity, while the interest rates, market conditions, and other factors keep changing constantly.
- If the NPV computation works well, it adds to the reputation of the company or shareholder, or investor. On the other hand, if things fail, the reputation gets highly hampered.
Frequently Asked Questions (FAQs)
What is a discount rate?
What are the types of discount rates?
How are NPV and discount rate related?
