Discount Factor
Last Updated :
21 Aug, 2024
Blog Author :
N/A
Edited by :
N/A
Reviewed by :
Dheeraj Vaidya
Table Of Contents
What is the Discount Factor?
Discount Factor is a weighing factor that is most commonly used to find the present value of future cash flows and is calculated by adding the discount rate to one which is then raised to the negative power of a number of periods.
Table of contents
- The discount factor is a financial term used to calculate the present value of future cash flows. It represents the factor by which future cash flows are reduced to reflect the time value of money.
- The discount factor considers the period and the discount rate. The discount rate is typically a predetermined return or interest rate representing the cost of capital or the opportunity cost of investing elsewhere.
- The discount factor is used in various financial calculations, such as net present value (NPV), discounted cash flow (DCF) analysis, and bond pricing.
- The discount factor is inversely related to the discount rate and period. As the discount rate increases or the period lengthens, the discount factor decreases, resulting in a lower present value for future cash flows.
Discount Factor Formula
Mathematically, it is represented as below,
where,
- i = Discount rate
- t = Number of years
- n = number of compounding periods of a discount rate per year
In the case of continuous compounding formula, the equation is modified as below,
Discount Factor Formula Explained in Video
Calculation (Step by Step)
It can be calculated by using the following steps:
- Firstly, figure out the discount rate for a similar kind of investment based on market information. The discount rate is the annualized rate of interest, and it is denoted by i
- Now, determine how long the money is going to remain invested, i.e., the tenure of the investment in terms of several years. The number of years is denoted by t
- Now, figure out the number of compounding periods of a discount rate per year. The compounding can be quarterly, half-yearly, annually, etc. The number of compounding periods of a discount rate per year is denoted by n (The step is not required for continuous compounding)
- Finally, in the case of discrete compounding, it can be calculated using the following formula as,
DF = (1 + (i/n))-n*t
On the other hand, in the case of continuous compounding, it can be calculated using the following formula as,
DF = e-i*t - On the other hand, in the case of continuous compounding, it can be calculated using the following formula as,
DF = e-i*t
Examples (with Excel Template)
Example #1
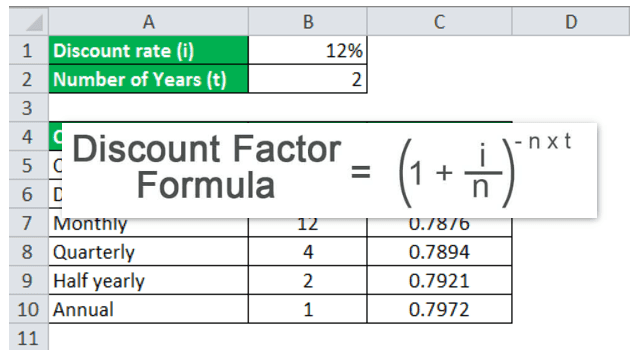
Let us take an example where the discount factor is to be calculated for two years with a discount rate of 12%. The compounding is done:
- Continuous
- Daily
- Monthly
- Quarterly
- Half Yearly
- Annual
Given, i = 12% , t = 2 years
#1 - Continuous Compounding
The formula = e-12%*2
- DF = 0.7866
#2 - Daily Compounding
Since Daily Compounding, therefore, n = 365
= (1 + (12%/365))-365*2
= 0.7867
#3 - Monthly Compounding
Since monthly compounding, therefore n = 12
The calculation of the DF is done using the above formula as,
= (1 +(12%/12))-12*2
= 0.7876
#4 - Quarterly Compounding
Since quarterly compounding, therefore n = 4
The calculation of the DF is done using the above formula as,
= (1 + (12%/4))-4*2
= 0.7894
#5 - Half Yearly Compounding
Since half yearly compounding, therefore n = 2
= (1 + (12%/2))-2*2
= 0.7921
#6 - Annual Compounding
Since annual compounding, therefore n = 1,
The calculation of the DF is done using the above formula as,
= (1 + (12%/1))-1*2
= 0.7972
Therefore, the Discount Factor for various compounding periods will be -
The graphical representation of the above table will be as follows -
The above example shows that the formula depends not only on the rate of discount and the tenure of the investment but also on how many times the rate compounding happens during a year.
Example #2
Let us take an example where the discount factor is to be calculated from year 1 to year 5 with a discount rate of 10%.
Therefore, the calculation of DF from year 1 to year five will be as follows -
- DF for Year 1 = (1 + 10% )-1 =0.9091
- DF for Year 2 = (1 + 10% )-2 = 0.8264
- DF for Year 3 = (1 + 10% )-3 = 0.7513
- DF for Year 4 = (1 + 10% )-4 = 0.6830
- DF for Year 5 = (1 + 10% )-5 = 0.6209
Therefore, DF of Year 1 to Year 5 is shown in the below figure -
The above example captures the dependence of DF on the tenure of the investment.
Discount Factor Calculator
Use and Relevance
Understanding this discount factor is very important because it captures the effects of compounding on each time period, which eventually helps in the calculation of discounted cash flow. The concept is that it decreases over time as the effect of compounding the discount rate builds over time. As such, it is a very critical component of the time value of money.
It is the decimal representation used in the time value of money for cash flow. To determine the discount factor for cash flow, one is required to assess the highest interest rate one can get on an investment of a similar nature. Consequently, investors can utilize this factor to translate the value of future investment returns into present value in dollars.
Frequently Asked Questions (FAQs)
The discount factor can be calculated using the formula: Discount Factor = 1 / (1 + r)^n, where "r" is the discount rate and "n" is the number of periods.
The discount factor is derived from the discount rate. A higher discount rate results in a lower discount factor, while a lower discount rate leads to a higher one.
In NPV calculations, the discount factor is multiplied by each future cash flow to convert it into its present value. The current values of all cash flows are then summed up to calculate the NPV.
The discount factor is always a positive value because it represents the present value factor used to reduce future cash flows to their current value equivalents. Negative cash flows are typically characterized by negative values in the calculations.
Recommended Articles
This article has been a guide to Discount Factor Formula. Here we discuss how to calculate the Discount Factor using practical examples along with downloadable excel templates. You may learn more about Financial Analysis from the following articles –
- Cohort Analysis
- Calculate Perpetuity
- Calculate Discounted Payback Period
- DDM
- Incremental IRR
support@wallstreetmojo.com