Descriptive Statistics

Descriptive statistics refers to the analysis of data. Sample data is summarized using charts, tables, and graphs. Quantitative analysis is difficult when the population is large. Therefore, a small data sample is interpreted.

This data set is well-formatted and divided structurally. A relation between two data variables or a common average is established. This is followed by inferential statistics. Inferential statistics determines whether the conclusions hold true for the whole population or not.

• Descriptive statistics refers to the collection, representation, and formation of data. It is used for summarizing data set characteristics.
• It is classified into three types—frequency distribution, central tendency, and variability.
• Descriptive analysis is widely applied in different fields for data representation and analysis. Descriptive statistics and inferential statistics are significant components of quantitative research.

Statistics transforms raw data into meaningful results. It is the science behind the identification, collection, organization, interpretation, and presentation of data. Data could be qualitative or quantitative. Statistics makes information-based decision-making easier.

Descriptive statistics merely describes and summarizes collected data. In contrast, inferential statistics draws conclusions about the population at large using data.

Whenever there is a large population, the probability of making an error increases. And this needs to be dealt with. In addition, researchers face challenges like data distortion, recalculation, and missing figures. This is where descriptive statistics come into play—a small data sample is taken and summarized.

It is a powerful tool to analyze and represent data for calculation and analysis. As a result, it is extensively used in science, business, commerce, and medicine.

Descriptive statistics is further classified into the following types:

#1 - Frequency Distribution

Frequency distribution refers to the number of times a particular aspect is accounted for. It is primarily recorded and denoted in a tabular format and used for qualitative and quantitative data analysis.

Let us assume that a school takes a group of students to picnic every year. Some of the students have already visited the picnic spot before; they are visiting the picnic spot for the second time. Some students have visited the picnic spot more than two times as well. Here, students are divided based on the number of visits. The number of visits, therefore, denotes the frequency distribution among the students.

Similarly, any process or data sample, when recorded for the total number of times it occurred, is called a frequency distribution sample.

#2 - Central Tendency

Central tendency comprises three methods of calculation:

1. Mean
2. Median
3. Mode

The results reflect the central value of a data set—to be used as an aggregate of the total number of counts or occurrences. Mean refers to the most common average value of the occurrence, median denotes the data sample's central or middle score, and mode represents the most frequent value.

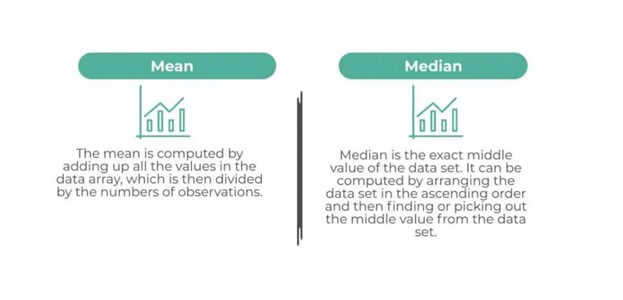
So, if the average number of visits to the picnic spot is three, the data mean value is also three. Among different frequencies, two is the middle score for the number of visits and therefore attributed as the median. Also, if one is the most common number of visits among the student, the sample mode is one.

#3 - Variability

Variability explains the extent to which data points are dispersed from each other. It also designs a range of dispersion and the degree of variance occurring in the data sample from its highest to its lowest value.

For example, the lowest number of visits to the picnic spot is one. The highest number of picnic spot visits is 4. Variability creates a range that derives how far each value is from the central tendency. The range itself is the degree of dispersion.

Using statistical tools like range, standard deviation, and variability, different components of data sample are determined.

Let us look at some examples to understand the application of the methods.

Example #1

The data collected for COVID19 vaccine hesitancy in Austria is a good example of descriptive statistics.

The study has a sample size of 1543—researchers recorded 1543 unvaccinated citizens. The interpretation highlighted the most common reasons for hesitation—fear of side effects, the desire to have children, the assumption that the immune system is enough, spiritual beliefs, conspirational thinking, and low trust in societal institutions.

Example #2

In 2022, text analytics was used in the evaluation of running backs' positions. Data from the last eight seasons were considered, and prospect scores were created. The analysis enabled player comparison for a particular criterion (prospect score). Based on the prospect scores, players were ranked separately for each position.

The two statistical approaches differ in the following ways:

• Descriptive statistics summarizes raw data information in a tabular format to test the hypothesis. In contrast, inferential statistics makes inferences based on collected data.
• Descriptive analysis is used for the organization and presentation of data in a meaningful manner. Inferential statistics, on the other hand, compares data, runs hypotheses, and makes predictions.
• Descriptive analysis merely depicts a situation. Inferential statistics ventures further; it is used to make conclusions. Researchers use inferential statistics to predict possibilities, probabilities, and the occurence of events.
• Characteristically, descriptive analyses consider small data. Inferential statistics is used to apply the findings to the whole population.
• For description, researchers use charts, graphs, and tables. In inferential statistics, researchers use probability to draw conclusions.

This has been a Guide to What is Descriptive Statistics & its Definition. We explain its types, examples, quantitative descriptive analysis & descriptive statistics vs inferential statistics. You can learn more about statistics from the articles below –

• Standard Error
• Multicollinearity
• Decile