Table Of Contents
What Is Daily Compound Interest?
Daily compounded interest means interest is accumulated daily and is calculated by charging interest on principal plus interest earned daily; therefore, it is higher than interest compounded on a monthly/quarterly basis due to the high frequency of compounding.
Many investment opportunities and financial institutions follow this method. It is widely used in the case of trading with margin money, like in the case of options trading, forex trading, or commodities. This comes with great risk. However, such a method allows deposits or loans to increase faster, proving beneficial for lenders but difficult for borrowers.
Table of contents
- Daily compounded interest denotes that interest is accrued daily and determined by charging interest on principal plus daily interest. It is more than interest compounded monthly or quarterly due to the high compounding frequency.
- Credit card spending is subject to daily compounding, which banks charge credit card customers. It frequently features a 60-day grace period during which no interest is set, but interest is charged if the interest is not paid within 60 days.
- When one borrows money from a bank, the bank charges the borrower daily compounded interest. The more frequent the payment, the higher the interest charged or paid on the principle.
Daily Compound Interest Explained
Daily Compound Interest is the process of compounding the money on a daily basis. A certain rate of interest is added daily on the principal and the interest added the previous day. In this way when we calculate daily compound interest, the total amount grows at a much faster rate and becomes beneficial in certain cases but difficult for some.
The frequency of compounding may be different for different financial institutions, but some strictly follow the daily method. Lenders who follow this policy find it hugely profitable because the money grows quickly. But for investors who invest in opportunities that have this kind of interest calculation also finds it beneficial since their investment multiplies very fast.
In this process, where we calculate daily compound interest, the wealth multiplies exponentially. The interest earned is added to the previous day’s interest plus principal, Thus, the process adds back the earned profit to the previous amount and then the reinvestment is done. This accelerates the process of returns. generated from the investment.
Formula
Let us look at the formula used to calculate the daily compound interest equation and understand it in details.
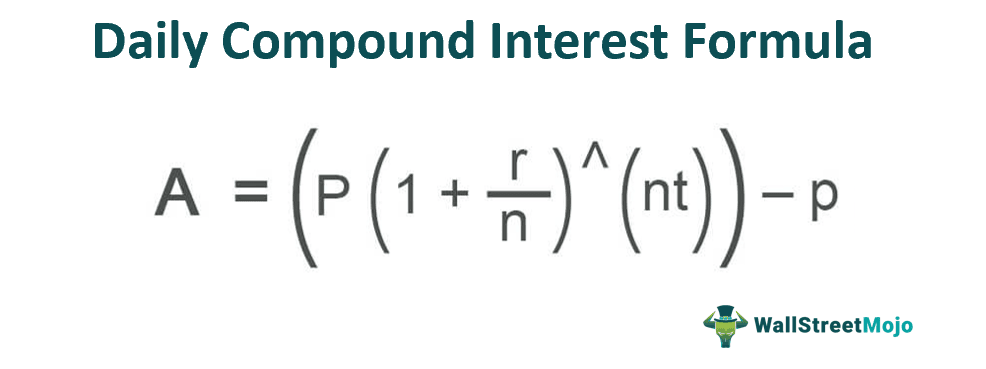
Where
- A=Daily compound rate
- P=Principal amount
- R=Rate of interest
- N=Time period
Generally, when someone deposits money in the bank, the bank pays interest to the investor in quarterly interest. But when someone lends money from the banks, the banks charge the interest from the person who has taken the loan in daily compounding interest. This scenario is mostly applicable in the case of credit cards.
Thus, we see that financial institutions often use this method of daily compound interest equation for their own benefit so that their profitability increases, and they have more funds at their disposal for lending. This leads to good financial stability and an increase in the customer base for lending. But as mentioned above, very often, investments are not subject to daily compounding, proving a loss for the investors. From here we can see that financial institutions use this method for double gain from both sides.
Compound Interest Examples in Video
Examples
Let us look at some suitable examples to understand the concept of daily compound interest accounts in details.
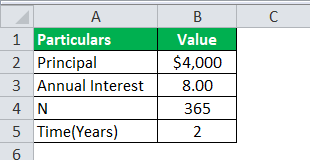
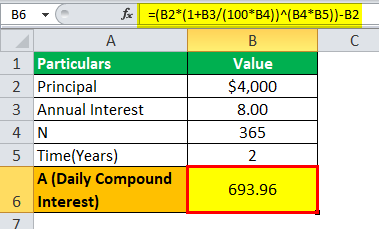
Example #1
A sum of $4000 is borrowed from the bank, where the interest rate is 8%, and the amount is borrowed for two years. Let us determine how much will be daily compounded interest calculated by the bank on loan provided.
Solution:
= ($4000(1+8/365)^(365*2))-$4000
Example #2
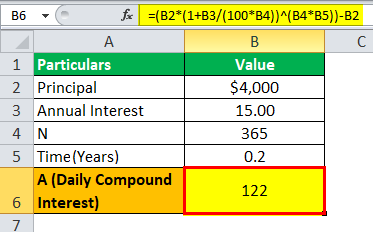
Daily compounding is practically applicable for credit card spending, which the banks charge to the individuals who use credit cards. Credit cards generally have a cycle of 60 days, during which the bank does not charge any interest, but interest is charged when the interest does not pay back within 60 days. If a sum of $4000 is used using a credit card by an individual for its spending. And the interest rate is 15% per annum as the interest charged for a credit card is generally very high. And the amount is repaid by the individual after 120 days, that is, 60 days after the grace period is over. So the individual needs to pay the bank interest for 60 days, and he is charged at a daily compounding rate.
Solution:
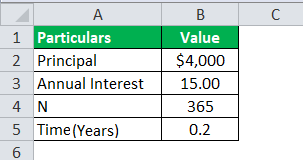
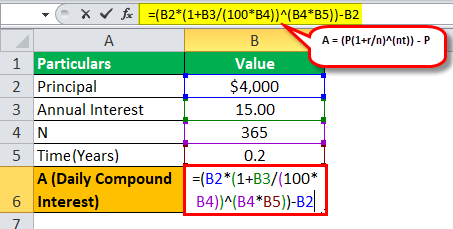
= $4000(1+15/365)^(365*(12/60))-$4000
Example #3
A sum of $35000 is borrowed from the bank as a car loan where the interest rate is 7% per annum, which is borrowed for five years. Let us determine how much will be daily compounded interest calculated by the bank on loan provided.
Solution:
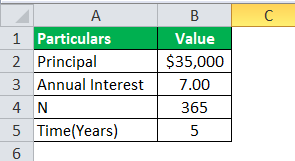
= ($35000(1+.07/365)^(365*5))-$35000
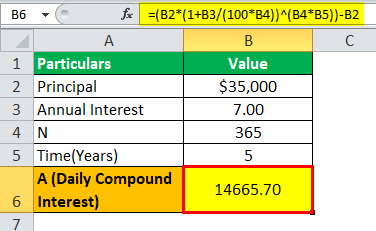
From the above examples, we learn how this concept of daily compound interest accounts is widely used in different scenarios for compounding purposes. We also learn how these different situations result in the funds getting compounded and the resultant benefit derived by different parties to the transactions.
Relevance And Use
We learn the different uses of the concept of daily compound interest investments as given below:
It has already been discussed how the banks use this daily compound interest investments to multiply their deposits and funds in two different ways. From here we can conclude that it is highly beneficial for them because of higher fund inflow within a short time, which they can use to lend further. In this way the cycle continues and leads to accumulation of large corpus for financial business.
The higher the frequency, the more interest is charged or paid on the principal. It is how the banks make their money on the differential of the interest.
You can download this template from here – Excel Template
Daily Compound Interest Vs Monthly Compound Interest
It is important to understand the difference between the two types of compounding methods followed in the financial market. Let us understand the difference as given below:
- For the former, the compounding in done on a regular basis but in case of the latter, the same is done on a monthly basis.
- From the above point is can be derived that for the former, an investment will receive interest 365 times in a given year, but in case of the latter, the same investment will receive interest 12 times in a given year.
- Comparatively, the former is a situation where the fund will accelerate at a faster rate than the latter.
- In case of lending, the lender will find the former concept profitable since they will receive more money, but the latter is not.
- In case of investments, the investor will find the former more profitable but not the latter.
Thus, these differences are to be kept in mind before selecting the interest type either for investment or for borrowing.
Frequently Asked Questions (FAQs)
Compounding daily outperforms compounding monthly. The shorter the compounding time, the higher the effective yield.
Excel's general interest formula is more efficient for computing compound interest. FV = PV(1+r)n, where FV represents future value, PV represents current value, r represents the interest rate per period, and n represents the number of compounding periods.
Generally, when someone deposits money in a bank, the bank pays the investor quarterly interest. However, when someone borrows money from a bank, the bank charges the borrower interest in the form of daily compounding interest.
Simple interest is calculated only on the initial principal amount, whereas daily compound interest considers both the principal and the accumulated interest. This results in faster growth of the account balance with daily compounding.
Recommended Articles
This article is a guide to what is Daily Compound Interest. We explain formula, differences with monthly compounded interest along with examples & uses. You can learn more about financial analysis from the following articles –
