Coupon Bond Formula

The term “coupon bond” refers to bonds that pay coupons which is a nominal percentage of the par value or principal amount of the bond. The formula for calculation of the price of this bond basically uses the present value of the probable future cash flows in the form of coupon payments and the principal amount which is the amount received at maturity.

The present value is computed by discounting the cash flow using yield to maturity. However, in the formula, it is assumed that there are regular payments, which is typically semi annual. The formula is adjusted if the time interval is different. This formula calculates the interest paid to bondholders till the financial instrument reaches its maturity date.

The coupon rate formula for bonds is the method used to calculate the interest given out to bondholders at different interval of time. Bonds are a type of financial instrument that the issuer uses to raise money from investors in the form of debt. The issuer needs to repay the amount of the bond at maturity along with regular interest payments which are also known as coupons.

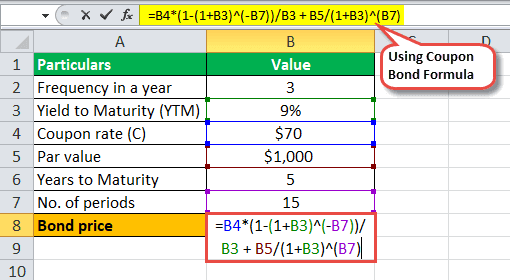
Mathematically, it the price of a coupon bond is represented as follows,

where

• C = Periodic coupon payment,
• P = Par value of bond,
• YTM = Yield to maturity
• n = No. of periods till maturity

The periodic payment of coupons are made at a fixed amount as per the interest rate mentioned on the face value of the bond. This may be paid out semi-annually or annually.

The par value, which is also called the face value of the debt instrument in the money that the holder of the bond will get at the time the financial instrument reaches the maturity date.

The yield to maturity is the term that explains the total amount of return that may be expected from a bond when the bondholders keep it till maturity. It is the rate of return on investment in a bond with the assumption that the coupon payments are made regularly, and they are immediately reinvested.

In the present value of coupon bond formula, the period till maturity refers to the total number of coupon periods left till maturity. In other words, it is the length of time during which the owner will continue getting coupon payments from the bond issuer. The principal is repaid back to the bondholder at maturity.  

Let us understand the concept of coupon rate formula for bonds with the help of some suitable examples.

Example #1

Let us take an example of bonds issued by company XYZ Ltd that pays coupons annually. The company plans to issue 5,000 such bonds, and each bond has a par value of $1,000 with a coupon rate of 7%, and it is to mature in 15 years. The effective yield to maturity is 9%. Determine the price of each bond and the money to be raised by XYZ Ltd through this bond issue.

Below is given data for the calculation of the coupon bond of XYZ Ltd.

The price of each bond is calculated using the below formula as,

Therefore, calculation of the Coupon Bond will be as follows,

So it will be –

= $838.79

Therefore, each bond will be priced at $838.79 and said to be traded at a discount (bond price lower than par value) because the coupon rate is lower than the YTM. XYZ Ltd will be able to raise $4,193,950 (= 5,000 * $838.79).

Example #2

Let us take an example of bonds issued by company ABC Ltd that pays semi-annual coupons. Each bond has a par value of $1,000 with a coupon rate of 8%, and it is to mature in 5 years. The effective yield to maturity is 7%. Determine the price of each C bond issued by ABC Ltd.

Below is given data for the calculation of the coupon bond of ABC Ltd using the present value of coupon bond formula.

Therefore, the price of each bond can be calculated using the below price of coupon bond formula as,

Therefore, calculation of the Coupon Bond will be as follows,

So it will be –

= $1,041.58

Therefore, each bond will be priced at $1,041.58 and said to be traded at a premium (bond price higher than par value) because the coupon rate is higher than the YTM.

The above examples clearly explain how the financial information of bond issue is used to calculate the interest amount or the coupon payment made to bondholders. Thus, the price of coupon bond formula helps in assessing the level of regular income that the investor can expect to receive from the debt instrument and accordingly decide whether it is profitable to invest in it or not.  

Let us understand how the formula is relevant in the financial  market and how it is useful for earning regular income.

• The most important use of the annual coupon bond formula is that it helps in calculating the market value of the bond which in turn helps in assessing how worthy the investment will be. It is frequently used by analysts, investors and financial institutions what is its value in the secondary market.
• The concept of pricing of this kind of bond is very important from the perspective of an investor because bonds are an indispensable part of the capital markets. The purchaser of a bond receives these coupon payments during the period between the issuance of the bond and the maturity of the bond.
• In the bond market, bonds with higher coupon rates are considered to be more attractive for investors because they offer higher yields.
• Further, bonds trading at a value higher than their par value are said to be traded at a premium, while the bonds trading at a value lower than their par value are said to be traded at a discount. Nowadays, these bonds are quite uncommon because most recent bonds are not issued in coupon or certificate form. Rather the bonds are issued electronically.
• It helps investors make informed financial decisions as per their risk-taking ability, investment horizon, and financial goals. If the risk appetite of the investor is less, bonds are a very profitable investment for them due to their regular income and very low risk.
• The interest rate risk can be assessed using the formula. The price of the coupon bond which varies as per variation in interest rates is a very important concept. The bond price will change with the market rates which provides valuable information and insight to investors and analysts regarding how sensitive the bond is to market movement.
• Investors often use the formula to compare different investment options among bonds themselves to decide which is the best alternative or which will provide more return in future.
• It also helps traders who trade in bonds to identify opportunity for profits.
• In case of the issuer, the formula provides the cost of borrowing when new bonds are issued at a particular coupon. This ensures that the cost of debt does not become a burden for the issuer.