Conditional Probability

Conditional probability refers to the chances of a particular event occurring, provided another event has previously occurred. It is widely applicable in many areas, including business risk management, insurance, personal life, calculus, politics, etc., helping individuals and entities identify possible outcomes and make practical decisions accordingly.

This estimation could either be assumption-based or evidence-based, depending on the nature of the outcome desired or expected. Its mathematical formula involves the multiplication of the probability of the previous event (B) by the chances of the next event (A) occurring. Decision-makers, policymakers, engineers, data scientists, and other professionals use this method to determine the likelihood of a specific event or outcome occurring.

• Conditional probability expresses the chances of whether a particular event will take place based on another previously happened outcome. It is a crucial part of probability theory but different from unconditional probability.
• It is of great importance for decision-makers, policymakers, engineers, data scientists, and other professionals to determine the probable outcome of a plan, decision, or action.
• The conditional probability rules could either be assumption-based or evidence-based and are different for independent and mutually exclusive events.
• The Bayes Theorem is nothing but the mathematical formula for conditional chance or probability. It got its name from Thomas Bayes, a notable 18th-century British mathematician.

Both in professional and personal life, one likes to have an idea of what might or might not happen in a given situation based on another event that has already occurred. Conditional chance or probability can tell one about the likelihood of an outcome based on the conditions dominating a previous occurrence.

It is an essential component of probability theory. However, it is different from unconditional probability, where the chances of an event occurring do not depend on the previous outcome or condition.

The mathematical formula used to calculate the probability of outcome A depending on the condition B is:

P(A) = P(A|B)

Several conditional probability examples show how the concept can help deduce an event's probability. Let us consider two cases to understand it better:

Conditional Probability Of Independent Events

An independent event occurs when the outcome or condition of the previous (B) or subsequent (A) event has no bearing on either. Hence, the formula is:

P(A|B) = P(A)

Let us find out the probability of one card being Jack (J) from the deck of 52-cards.

• There are four Jacks in the deck of those well-shuffled cards.
• The probability of a player getting a Jack is 4/52 or 1/13.

However, As soon as the condition of the Jack cards being Red (R) gets introduced, the above example turns into a conditional chance or probability.

• In that case, the number of red Jacks in the deck is two, and the total number of red cards is 26, given the rest of the 26 cards being black.
• After applying the condition with relation to the probability of the previously occurred event, the conditional chance of the Jack card belonging to the red suits comes to 2/26 or 1/13 again.

The events occurring here are said to be independent of each other as the likelihood of a card being both red and Jack has no influence on each other in any manner. Hence, the conditional probability calculation would be as follows:

P(J|R) = P(J)

Where,

• P(J|R) = Probability (Card be Jack|Must be Red)
• J - The card is a Jack
• R - The card is Red

P(J|R), where the letter on the right side of the bar denotes the event while on the left side of the bar is the condition driving the equation.

Conditional Probability Of Mutually Exclusive Events

It is the situation where one event negates the probability of the occurrence of the other event. Tossing a coin is a prominent example of this. If a person obtains Heads (H) on tossing a coin, there is no chance of getting a Tail (T) at that moment. In other words, whoever tosses the coin, will get either side, but never both at that moment.

Since these two events cannot simultaneously occur, their conditional chance or probability will always be zero. It means, in a mutually exclusive situation:

P(H|T) = 0

P(T|H) = 0

The conditional probability formula for an event that is neither mutually exclusive nor independent is:

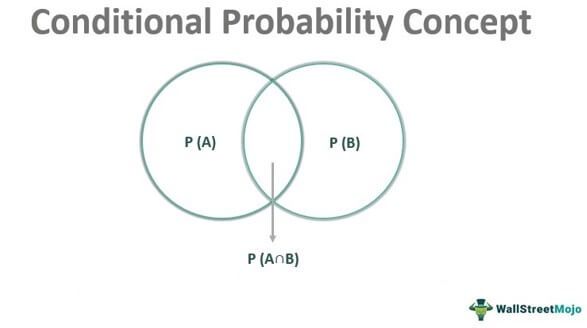
P(A|B) = P(A∩B)/P(B), where:

• P(A|B) denotes the conditional chance, i.e., the probability of the occurrence of event A with relation to condition B.
• P(A∩B) signifies the joint probability of both events occurring. It is not what both the events cover individually but the common factor that connects both of them for the outcome.
• P(B) is the probability of B.

Let us check out the conditional probability calculation part using this formula in the following section.

Example #1

• B1 and B2 are the two boxes.
• The first box contains five squash balls - three blue and two green.
• The second box has seven squash balls - one blue and six green.

Karl draws a squash ball from each box randomly. How likely is Karl to choose –?

1. A blue squash ball (B)
2. A green squash ball (G)
3. Green squash ball (G) from B2

Solution

Total number of squash balls (B1+B2) = 5+7 = 12

• The probability of a blue squash ball to be chosen = No. of blue squash balls/Total no. of squash balls

P(B) = (3+1)/12 

= 4/12

= 1/3

• The probability of a green squash ball to be chosen = No. of green squash balls/Total no. of squash balls

P(G) = (2+6)/12 

= 8/12

= 2/3

• Probability of a green squash ball to be chosen from B2 = No. of green squash balls in B2/Total no. of squash balls in B2

P(G|B2) = 6/7

The third scenario is an example of conditional chance or probability where event G needs to be figured out based on condition B2.

Example #2

In a book fair attended by 300 people, 130 bought fiction books (F). Seventy people chose non-fiction books (N), while 100 visitors selected books from both genres. If a randomly chosen buyer bought a fiction book, what is the probability of the same person buying a non-fiction book too?

Solution

• Probability of people choosing fiction books, i.e., P(F) = 130/300

= 0.43

• Probability of people choosing fiction and non-fiction books, i.e., P(N∩F) = 100/300

= 0.33

Probability of a random person with fiction books also choosing non-fiction, i.e.,

• Probability of a random person with fiction books also choosing non-fiction, i.e., P(N|F) = P(F∩N)/P(F)

= 0.33/0.43

= 0.767 = 0.8 (approx.)

Therefore, the probability of a random buyer choosing non-fiction books given they have already purchased a fiction book is 80%.

Using conditional chance or probability helps individuals and entities understand what their efforts would result. As far as the Bayes Theorem is concerned, it is nothing but the mathematical formula named after British mathematician Thomas Bayes to calculate the probability. It helps determine individual conditional probabilities for preceding and succeeding events. Also, it provides a better chance for one event, given another event has occurred based on new or additional evidence.

Let us consider the following scenario to establish a relationship between conditional chance and Bayes Theorem. In the example, A and B are two events in a sample space. Thus, the probability of the occurrence of A given the already occurred event B and vice-versa would be:

P(A|B) = P(A∩B)/P(B) and P(B|A) = P(A∩B)/P(A)

After combining these two, the equation would be:

P (A∩B) = P (A|B)*P (B) = P (B|A)*P(A)

From the above, the next equation derived is:

P(A|B)* P(B) = P(B|A)*P(A)

P(A|B) = /P(B) ------------

This has been a guide to What is Conditional Probability and its Definition. Here we discuss formulas to calculate conditional probability and how it works, along with examples. You may also have a look at the following articles to learn more –

• A Priori Probability
• Probability Distribution
• Joint Probability Formula