Compounding

Compounding Definition

Compounding is the method of calculating total interest on the principal when the interest amount is earned and reinvested. In other words interest earned is accumulated to the principal amount depending on the time period of deposit or loan that can be monthly, quarterly or annually

Compounding Formula

Compounding formula is used to calculate total interest on the principal earned when the interest amount which is earned and reinvested and is calculated by principal amount multiplied by one plus rate of interest raise to the power number of periods less principal amount.

Compounding Formula = P [ (1+r)ⁿ – 1 ]

Where,

• C is the compound interest
• P is the principal amount
• r is the rate of interest
• n is the number of periods

You are free to use this image on your website, templates etc, Please provide us with an attribution linkHow to Provide Attribution?Article Link to be Hyperlinked
For eg:
Source: Compounding (wallstreetmojo.com)

It is very useful and is powerful when one wants to calculate compound interestCompound InterestCompound Interest is the interest earned from the initial Principal & the previously accumulated Interest amount. This is also known as “Interest on Interest” & it is always higher than the Simple Interest. read more. This equation takes into consideration the principal amount, the rate of interest, the frequency at which it shall pay an interest rate. The equation in itself compounds the interest amount, which is earned and reinvested. This gives the effect of multiplication, and the amount grows more than what growth it achieved in the earlier years. Hence, this is more powerful than the simple interest, which only pays with the same amount of interest every year.

Top 4 Examples of Compounding

Example #1

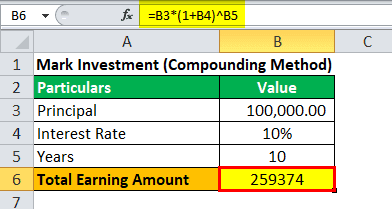
Shane and Mark both decided to invest $1,00,000, but Shane decided to invest in simple interest, whereas Mark invests in compound interest for ten years at 10% interest. Let see what happens after ten years.

Solution:

So, the calculation of Shane investment will be –

Total Earning Amount = $200,000

With a Simple interest, Shane will get $2,00,000 after 10 years.

The calculation of mark investment will be –

Total Earning Amount = $2,59,374

With Compound interest, Mark’s investment values will grow to $2,59,374.

Now Shane decided to invest through compounding methods like Mark, and they both invested $2,00,000 at the rate of 15%.

The calculation of Shane investment will be –

Total Earning Amount = $8,09,111.55

Shane stays invested for 10 years and gets the final amount as $8,09,111.55 at the rate of 15%.

The calculation of mark investment will be –

Total Earning Amount = $65,83,790.52

However, Mark is patience long-term investors and stays invested for 25 years, and his investment value grows to $65,83,790.52

The above example shows the power of compounding. The longer the investment horizonThe Investment HorizonThe term "investment horizon" refers to the amount of time an investor is expected to hold an investment portfolio or a security before selling it. Depending on the need for funds and risk appetite, the investor may invest for a few days or hours to a few years or decades.read more, the greater is the exponential growthExponential GrowthExponential Growth refers to the increase due to compounding of the data over time and follows a curve representing an exponential function. Exponential growth formula: Final value = Initial value * (1 + Annual Growth Rate/No of Compounding ) No. of years * No. of compoundingread more.

Example #2 (Weekly)

Simon is having $7500 in savings, and for his son’s college fund, who will be going to attend the college after 15 years, he decided to invest in US Savings Bonds. Simon’s goal is to save $20,000, and the annual percentage rate for a US saving bond is 6%. What is the Future Value of Simon Money after 15 years?

Solution:

Given,

• Principal = $7500
• Rate = 6% or 0.06
• Time Period = 15 years.
• How many times it’s compounded in a year n = 52 Weeks
• Future Value =?

So, the calculation of future value will be –

The formula for weekly compounding is as below.

• F = $7500(1+0.06/52)^52*15
• F = $7500(1+0.001153846)^780
• F = $18,437.45

So from the above calculation, it is clear that Simon’s goal to save $20,00 will not get achieved with the above methods, but it’s closer to that.

Continuous Compounding Method

Now let’s try the above example with Continuous Compounding FormulaContinuous Compounding FormulaThe continuous compounding formula depicts the interest received when constant compounding is done for an infinite number of periods. The four variables used for its computation are the principal amount, time, interest rate and the number of the compounding period.read more.

So, the calculation of future value will be –

• F = $7500e^0.06*15
• F = $7500e^0.9
• Future Value (F)= $18,447.02

Now even with Continuous Compounding, Simon’s goal of savings $20,000 for his son’s college fund will not be achieved.

Let’s see with Monthly compounded Formula that how much money did Simon need to invest to achieve his goal of saving $20,000 in 15 years at with an APR of 6%?

So, the calculation of future value will be –

• $20,000 = P(1+0.06/12)^12*15
• P = $20,000/(1+0.06/12)^12*15
• Principal (P) = 8149.65

So by Solving the above equation, we will get an answer that is $8,149.65 (Amount, which Simon needs to invest to achieve his goal of saving $20,000 in 15 years).

Example #3 (Effective Annualized Yield)

Let’s Say XYZ limited bank gives 10% per annum to Senior citizens for fixed deposit, and we assume here that bank interest is quarterly compounded like all other banks. Calculate the effective annualized yield for 5, 7, and 10 years.

Solution:

Annualized Yield for 5 Years:

• t = 5 years
• n = 4 (quarterly compounded)
• I = 10% per annum

So A = (1+10%/100/4)^ (5*4)

• A = (1+0.025)^20
• A = 1.6386
• I = 0.6386 in 5 Years

Effective Interest = 0.6386/5

Effective I = 12.772% Per Annum

Annualized Yield for 7 Years:

• t = 7 years
• n = 4 (quarterly compounded)
• I = 10% per annum

So A = (1+10%/100/4)^ (7*4)

• A = (1+0.025)^28
• A = 1.9965
• I = 1.9965 in 7 Years
• Effective I = 0.9965/7

Effective I = 14.236% Per Annum

Annualized Yield for 10 Years:

• t = 10 years
• n = 4 (quarterly compounded)
• I = 10% per annum

So A = (1+10%/100/4)^ (10*4)

• A = (1+0.025)^40
• A = 2.685
• I = 1.685 in 10 Years
• Effective I = 1.685/10

Effective I = 16.85% Per Annum

Example #4 – (Annuities: Future Value)

$1,000 is invested every 3 months at 4.8% per annum compounded quarterlyCompounded QuarterlyThe compounding quarterly formula depicts the total interest an investor can earn on investment or financial product if the interest is payable quarterly and reinvested in the scheme. It considers the principal amount, quarterly compounded rate of interest and the number of periods for computation.read more. How much will the Annuity be worth in 10 years?

Solution:

So when we say how much will the Annuity be worth in 10 years means here we have to find future value, and this important because whenever there is an example on annuities, we have to see what we have to find out.

So, the formula of Future Value is

• P = Periodic Payment
• r = Rate per period
• n = Number of periods

So the formula of Future Value is

• So here P = $1,000
• r = 4.8% Per Annum or 0.048
• r (quarterly) = 0.048/4
• r (quarterly) = 0.012
• n = 10 years
• n (Number of times compounding will apply) = 10×4 =40

So, the calculation of FV of Annuity will be –

So now FV = $1000[1+0.012]^40 -1/0.012]

So by Solving the above equation will get an FV of $50,955.30

So how much will be the Annuity in 10 years and answer is $50,955.30

As additionally, we can also find out from the above example that how much interest is earned in 10 years.

As 40 times $1000 is invested that is a total investment (40×$1000 = $40,000).

So Interest = Future Value – Total investment

• Interest = $50,955.30 – $40,000
• Interest = $10,955.30

So here, it is important to understand that in Annuities, investors can earn a lot of interest. In the above particular examples, a deposit of $40,000 gives, in return, a total interest of $10,955.30.

Recommended Articles

This has been a guide to what is Compounding & its definition. Here we understand the power of compounding with the help of practical examples. You may learn more about accounting from the following articles –

• Compound Interest Calculation
• Daily Compound Interest Calculation
• Simple Interest vs Compound Interest