Table Of Contents
About Compound Savings Calculator
The formula for calculating Compound Interest is:
Where,
- A is the initial Principal
- i is the interest rate
- F is the number of compounding periods which could be daily, annually, semi-annually, monthly or quarterly.
- n is the number of periods for which investment is to be made.
- I is the regular savings fixed amount.
This calculator calculates the amount received at maturity when the individual saves a certain amount and invests a fixed amount periodically. Some products could pay interest annually, monthly, quarterly, or semi-annually. Accordingly, this calculator will calculate the maturity amount the individual shall receive at the time of maturity. In this way, an individual will know about the amount he shall receive from the amount he has saved. If the individual compares various products, he can use this calculator to identify which one is paying better.
How to Calculate Using Compound Savings Calculator?
One needs to follow the below steps in order to calculate the amount for Retirement.
Step #1 - First, calculate the monthly savings an individual can make.
Step #2 - Determine the rate of interest that can be applied to the investment.
Step #3 - Now, Compound the initial amount either monthly, quarterly, semi-annually, or annually by the interest rate until the maturity period, as the case may be.
Step #4 - We now need to determine the future value of the monthly savings amount with the same rate of interest used to calculate an initial investment's maturity value.
Step #5 - Now, we can take a total of values arrived at in steps three and step 4, which shall be the future value of the savings invested.
Examples
Example #1
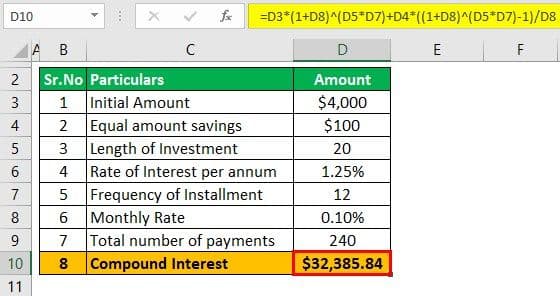
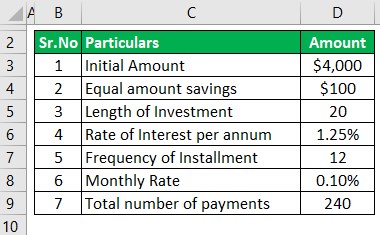
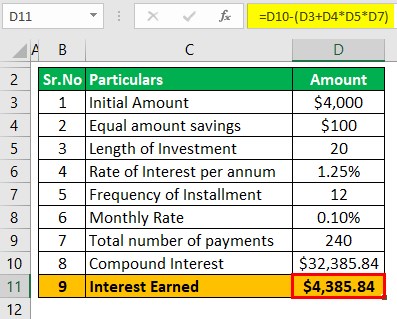
Kushal has been working with a startup company and earning quite well. Recently Mr. Kushal opened an account wherein he initially deposited $4,000, and he intends to save monthly $100 and deposit in this account. This account pays a 1.25% rate of interest which is compounded monthly. He intends to retain the same amount of savings until 20 years. Based on the given information, you are required to calculate the amount to be received at maturity.
Solution:
The following information is given: A is 4,000, and Interest Rate is 1.25%, which has to be divided by 12, which will be 0.10%, frequency is 12, and n is 20 as it's compounding monthly.
The formula for calculating Compound Interest is:
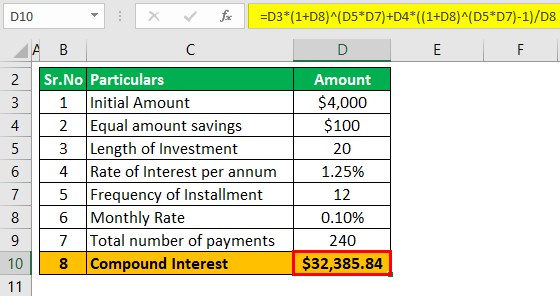
- = $4,000 *( 1 + 0.10% )20*12 + $100 *((1 + 0.10% )20*12 – 1) / 0.10%
- = $32,385.84
The income earned on this product will be $32,385.84 less (4000 + (100 * 12* 20)) which is $32,385.84 less $28,000 which is $4,385.84
Example #2
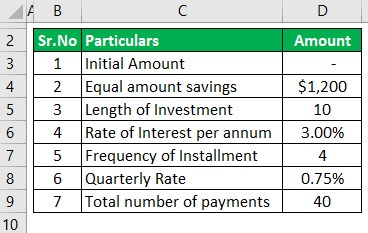
Booker has started saving $1200 per quarter and intends to invest the amount in an account which shall pay the interest rate of 3% per annum compounded quarterly. He intends to invest for ten years.
Based on the given information, you are required to calculate the amount to be received at maturity.
Solution:
The following information is given: A is 0, Interest Rate will be interesting is 3.00%, which, when divided by 4, will yield us 0.75%, frequency is 4, and n is ten as its compounding quarterly.
Here Mr. Booker saves $1200 per quarter.
The formula for calculating compound interest is:
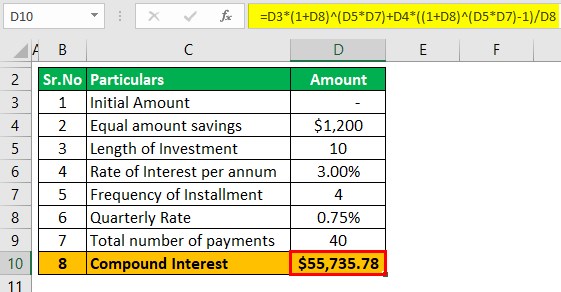
- = 0 * ( 1 + 0.75% )10*4 + $1200 * ( (1 + 0.75% )10*4 – 1) /0.75%
- = 55,735.78
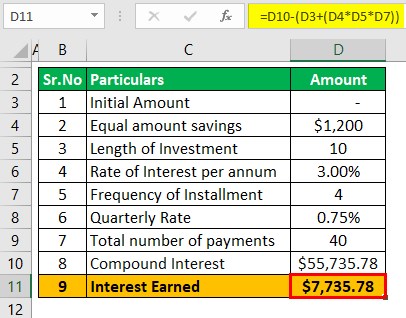
The income earned on this product will be $ 55,735.78 less (1200 * 4 * 10) which is $55,735.78 less $48,000 which is $7,735.78.
Conclusion
A compound savings calculator can be used to calculate the maturity amount of the savings that the individual has invested. He can know from the same how much he would be making in the future, assuming he doesn't withdraw any amount and could decide if it meets the goal or if he needs to invest more or further can reduce the same.