Coefficient Of Variation Formula

Last Updated :

Blog Author :

Edited by :

Reviewed by :

Table Of Contents

What Is The Coefficient Of Variation Formula?

The coefficient of variation formula refers to the statistical measure which helps measure the dispersion of the various data points around the mean. It is calculated by dividing the standard deviation by the mean and multiplying the resultant with 100.

Thus, it measures or expresses the variability within a set of data. It is a standard calculation that helps in the comparison of data having different means or different units and scales. If the formula gives a result where the value is less, it means the deviation is less and vice versa. The formula has a wide range of uses, including finance, economics, engineering, etc.

What Is The Coefficient Of Variation Formula?

Coefficient Of Variation Formula Explained

The term “coefficient of variation” refers to the statistical metric used to measure the relative variability in a data series around the mean or to compare the relative variability of one data set to that of other data sets, even if their absolute metric may be drastically different. Mathematically, the coefficient of variation formula represents as

Coefficient of Variation Formula = Standard deviation / Mean

One can further express formula for coefficient of variation as below:

Coefficient of Variation = √∑^N_i (Xi - X)² / X

where

X_i = i^th random variable
X= Mean of the data series
N = number of variables in the data series

Thus, we see from the above formula that it expresses the value in the form of a ratio of standard deviation to mean. However, it is mostly expressed as a percentage by multiplying the formula by 100. This facilitates comparison between two datasets since either because they may have different units of measurement or different means. The magnitude of variation relative to the average size can be easily expressed through this formula for coefficient of variation and direct comparison can be made. It has to unit of measurement.

How To Calculate?

Let us learn the steps of calculating coefficient of variation formula in excel with the help of the formula explained above.

One can do the calculation the coefficient of variation equation by using the following steps:

Firstly, figure out the random variables forming a large data series. Xi denotes these variables.
Next, determine the number of variables in the data series, denoted by N.
Next, determine the mean of the data series by initially summing up all the random variables of the data series and then dividing the result by the number of variables in the series. The sample mean is denoted by X.
Next, compute the data series's standard deviation based on each variable's deviations from the mean and the number of variables in the data series.
One may calculate the equation for the variation coefficient by dividing the data series's standard deviation by the series' mean.

Thus, we can easily use these steps for calculation. In case of any financial instrument, where calculation of return are extremely important, this method measures the value of risk, which is the standard deviation for each unit of the instrument or security against the return or reward of each unit, which is the mean return.

Example

Let us understand the concept of coefficient of variation formula in excel with the help of a suitable example.

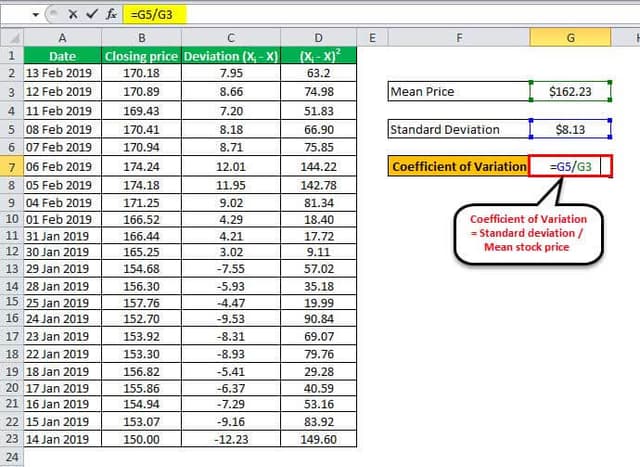
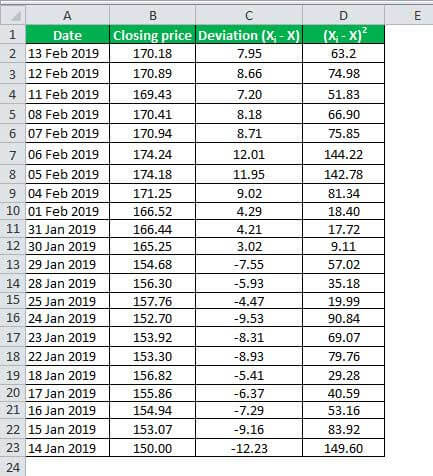
Take the example of Apple Inc.'s stock price movement from January 14, 2019, to February 13, 2019. Then, calculate the coefficient of variation for Apple Inc.'s stock price for the given period. Below is data for calculating the coefficient of variation of Apple Inc.

Below is data for calculation of the coefficient of variation of Apple Inc's

Calculation of Mean

On the based of the stock prices mentioned above, we can calculate the mean stock price for the period can be as,

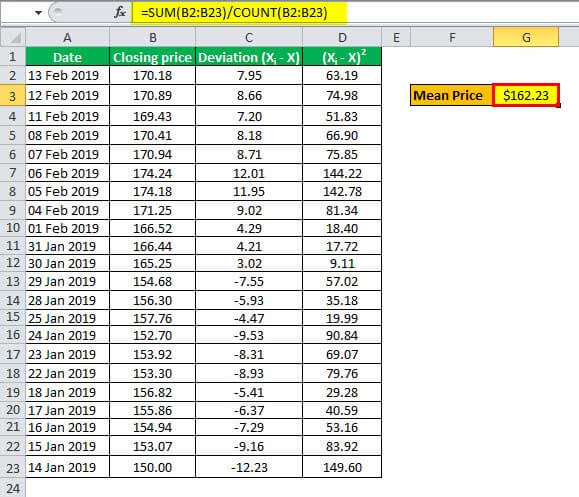
Coefficient of Variation Formula Example 1.1jpg

Mean stock price = Sum of stock prices / Number of days (add up all the stock prices and divide by the number of days. The detailed calculation is in the last section of the article)

= 3569.08 / 22

Mean = $162.23

Calculation of Standard Deviation

Next, determine the deviation of each stock price from the mean stock price. It is shown in the third column, while the square of the deviation is in the fourth column.

Now, one can calculate the standard deviation based on the sum of the squared deviations and the number of days as,

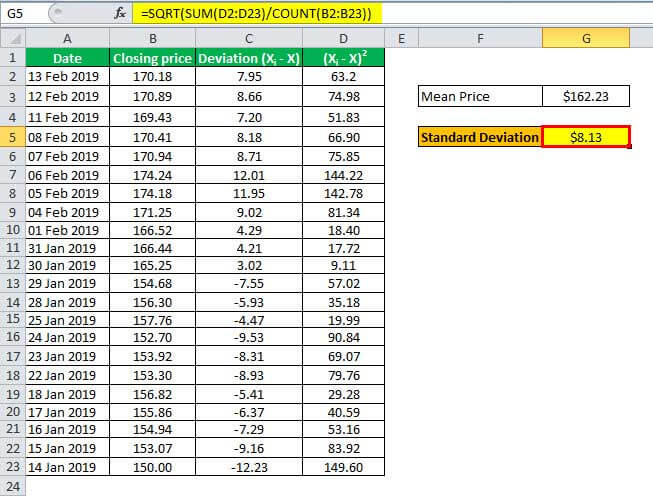
Standard deviation = (Sum of squared deviations / Number of days)^1/2

= (1454.7040 / 22)^1/2

Standard Deviation = $8.13

Coefficient Calculation

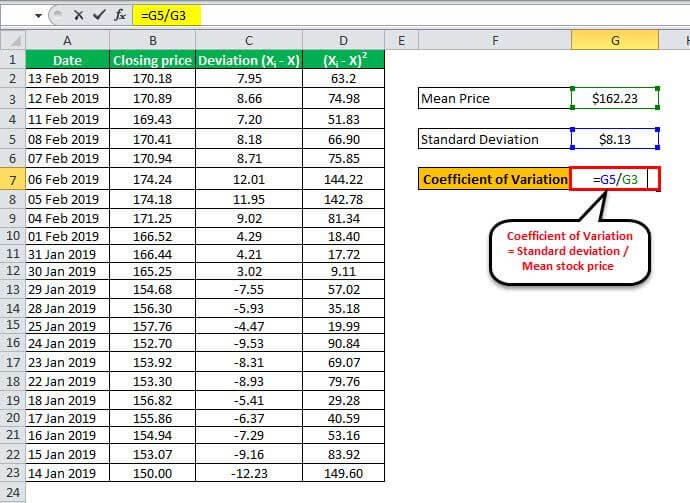
Coefficient of Variation Formula Example 1.3jpg

= $8.13 / $162.23

The coefficient will be -

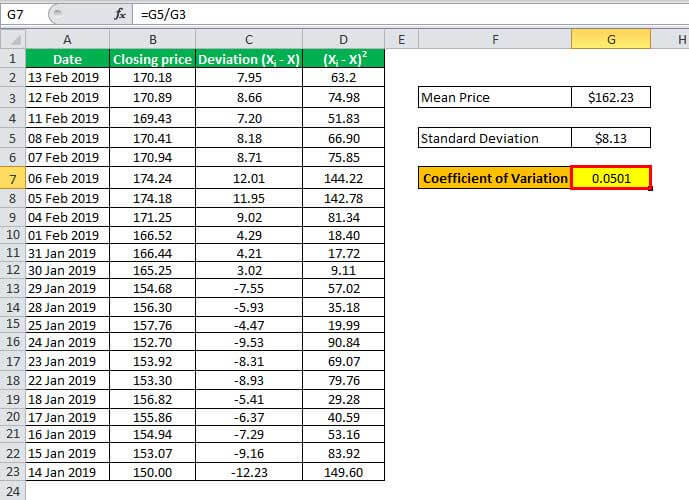
Therefore, the coefficient for Apple Inc.'s stock price for the given period is 0.0501, which can also express the standard deviation of 5.01% of the mean.

From the above example, we get a clear understanding of the concept of coefficient of variation formula in statistics and how it can be calculated systematically using the above steps.

Relevance And Use

The concept of coefficient of variation formula in statistics has important uses in the field of finance, engineering, technology, statistics, economic, biology, etc.

It is essential to understand the coefficient of variation formula concept because it allows an investor to assess the risk or volatility compared to the expected return from the investment. Please remember that the lower the coefficient, the better the risk-return trade-off. However, one limitation of this ratio is that if the mean or expected return is negative or zero, the coefficient could be misleading (since the mean is the denominator in this ratio).

This process of is helpful in case the two data sets have different units. In such cases, standard deviation is does not serve the purpose.
It is often used by investors who want to trade in exchange-traded funds (ETFs). It helps in better analysis of risk-return trade-offs.
The consistency of information can be verified using this method. In case the variation is more, the data can be assumed to be less consistent, which means the volatility is more.
From the above it can be derived that coefficient of variation formula for grouped data is useful in risk analysis. As mentioned above, if volatility of data is more, it also signifies sudden changes or higher risk in case of financial instruments. This is a valuable analysis and the formula acts as an essential tool in the financial market.
In certain industries, it can be used for quality analysis and control. A high variation also means deviation from the expected quality. The formula helps in such assessment.

Coefficient Of Variation Vs Standard Deviation

Both are statistical measures that evaluates the variability of a set of data. But they convey different ideas and results. Let us study the differences as given below:

The former gives a relative measure of variability, but the latter conveys an absolute measure between sets of data.
The coefficient of variation formula for grouped data allows the user of the formula to compare data which may have different means, but the latter just shows how much a particular datapoint will deviate from its mean.
The former expresses the the standard deviation of data as a percentage of the mean. But the latter shows the dispersion around mean.

Therefore, the above differences point out when and where to use both these concepts to get the best result.