Bond Pricing Formula

Publication Date :

24 Jan, 2019

Blog Author :

Edited by :

Reviewed by :

Download FREE Bond Pricing Formula Excel Template and Follow Along!

Bond Pricing Formula Excel Template.xlsx

Table Of Contents

Formula to Calculate Bond Price

The formula for bond pricing is the calculation of the present value of the probable future cash flows, which comprises the coupon payments and the par value, which is the redemption amount on maturity. The rate of interest used to discount the future cash flows is known as the yield to maturity (YTM.)

Bond Price = ∑_i=1ⁿ C/(1+r)ⁿ + F/(1+r)ⁿ

Bond Price = C* (1-(1+r)^-n/r ) + F/(1+r)ⁿ

Bond Price Formula

You are free to use this image on your website, templates etc, Please provide us with an attribution link

where C = Periodic coupon payment,

F = Face / Par value of bond,
r = Yield to maturity (YTM) and
n = No. of periods till maturity

On the other, the bond valuation formula for deep discount bonds or zero-coupon bonds can be computed simply by discounting the par value to the present value, which is mathematically represented as,

Zero-Coupon Bond Price = (as the name suggests, there are no coupon payments)

Key Takeaways

The bond pricing formula involves calculating the present value of the anticipated future cash flows, including coupon payments and the par value, or the amount redeemed when the bond matures.
The interest rate discounting future cash flows is called the "yield to maturity (YTM).
Bonds are an essential component of the financial markets, making bond pricing particularly significant. Analysts and investors must thus comprehend how a bond's many features interact to assess its underlying value.
Bond pricing is integral to bond investing since it helps determine if an investment suits a portfolio.

Bond Pricing Calculation (Step by Step)

The formula for Bond Pricing calculation by using the following steps:

Firstly, the face value or par value of the bond issuance is determined as per the company's funding requirement. The par value is denoted by F.
Now, the coupon rate, which is analogous to the interest rate of the bond and the frequency of the coupon payment, is determined. The coupon payment during a period is calculated by multiplying the coupon rate and the par value and then dividing the result by the frequency of the coupon payments in a year. The coupon payment is denoted by C.

C = Coupon rate * F / No. of coupon payments in a year
The total number of periods till maturity is computed by multiplying the years till maturity and the frequency of the coupon payments in a year. The number of periods till maturity is denoted by n.

n = No. of years till maturity * No. of coupon payments in a year
The YTM is the discounting factor, which is determined based on the current market return from an investment with a similar risk profile. The YTM is denoted by r.
Now, the present value of the first, second, third coupon payment, and so on so forth, along with the present value of the par value to be redeemed after n periods, is derived as,
Finally, adding together the present value of all the coupon payments and the par value gives the bond price as below,

Practical Examples (with Excel Template)

Example #1

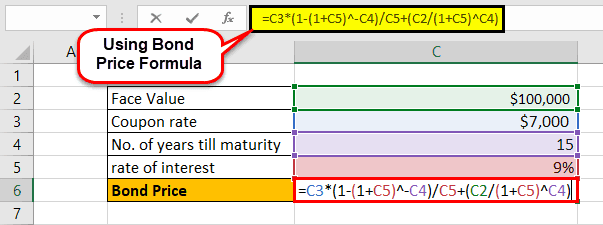
Let us take an example of a bond with annual coupon payments. Let us assume a company XYZ Ltd has issued a bond having a face value of $100,000, carrying an annual coupon rate of 7% and maturing in 15 years. The prevailing market rate of interest is 9%.

Given, F = $100,000
C = 7% * $100,000 = $7,000
n = 15
r = 9%

The price of the bond calculation using the above formula as,

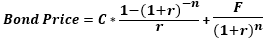
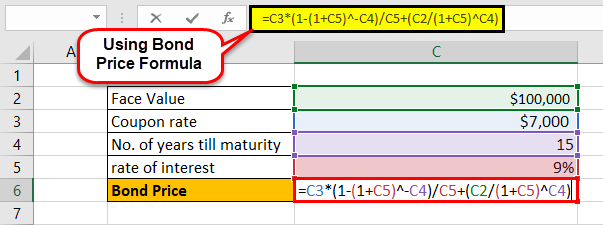
Bond price = $83,878.62

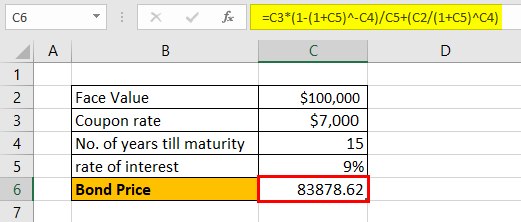
Since the coupon rate is lower than the YTM, the bond price is less than the face value, and as such, the bond is said to be traded at a discount.

Example #2

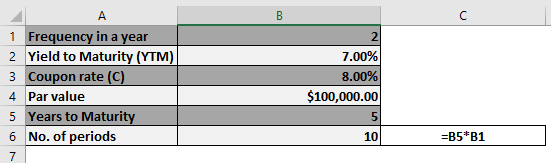
Let us take an example of a bond with semi-annual coupon payments. Let us assume a company ABC Ltd has issued a bond having the face value of $100,000 carrying a coupon rate of 8% to be paid semi-annually and maturing in 5 years. The prevailing market rate of interest is 7%.

Hence, the price of the bond calculation using the above formula as,

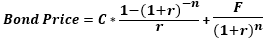
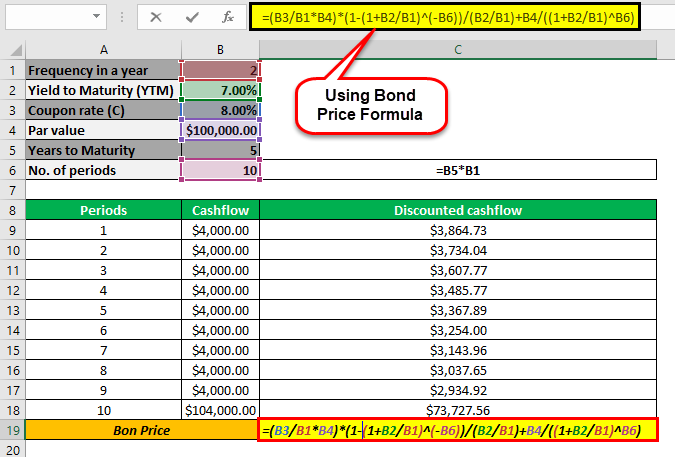
Bond price = $104,158.30

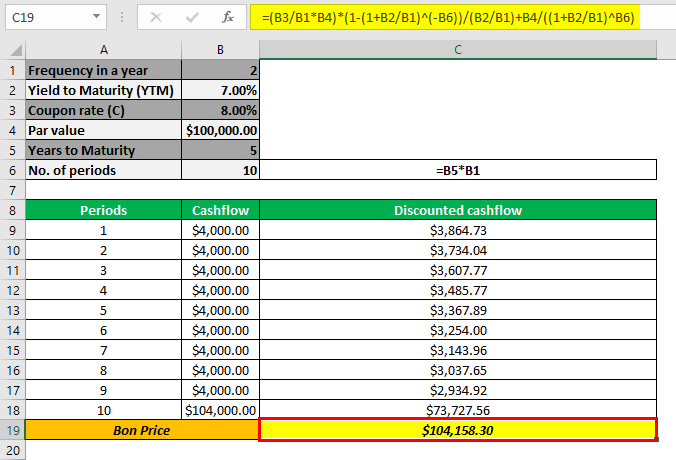
Since the coupon rate is higher than the YTM, the bond price is higher than the face value, and as such, the bond is said to be traded at a premium

Example #3

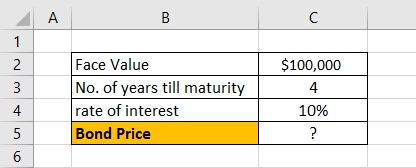
Let us take the example of a zero-coupon bond. Let us assume a company QPR Ltd has issued a zero-coupon bond with a face value of $100,000 and matures in 4 years. The prevailing market rate of interest is 10%.

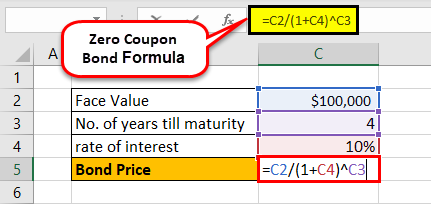
Hence, the price of the bond calculation using the above formula as,

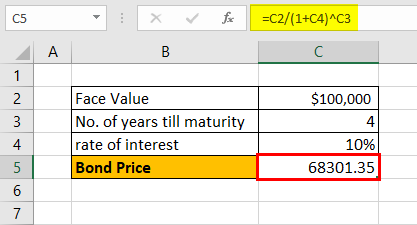
Bond price = $68,301.35 ~ $68,301

Use and Relevance

The concept of bond pricing is very important because bonds form an indispensable part of the capital markets. As such, investors and analysts must understand how a bond's different factors behave to calculate its intrinsic value. Similar to stock valuation, the pricing of a bond helps understand whether it is a suitable investment for a portfolio and consequently forms an integral part of bond investing.