Binomial Interest Rate Tree

A binomial interest rate tree is a financial tool representing the probability of the future increase or decrease in the short-term interest rate over the period through a tree diagram. It helps in pricing bonds and derivatives by determining their possible interest rate changes at each time interval.

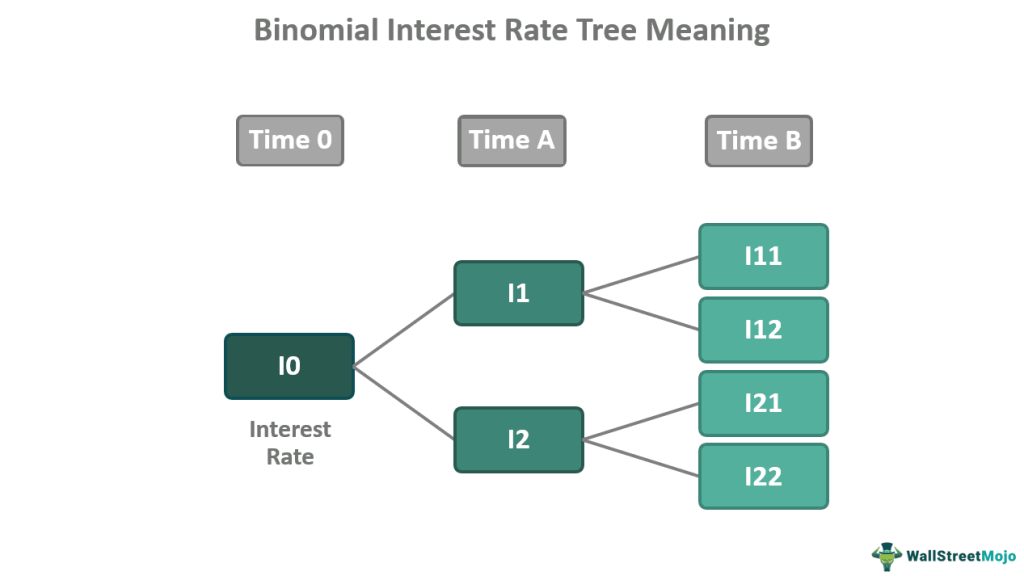
In finance, the binomial interest rate tree gauges the current value of an investment based on its expected periodic interest rate movement in the short run. It, thus, helps in sound investment decision-making in dynamic and complex financial scenarios. If p denotes the probability of an interest rate's upward movement, then its downward movement probability will be 1-p.

• A binomial interest rate tree is a tree-diagrammatic representation of the expected interest rate movement of an investment product or security, upward or downward, over the period at each interval.
• In finance, this tool is used for bond pricing, derivatives pricing, investment decision-making, and risk management in a volatile financial market.
• One of the known pricing models based on this phenomenon is the Black-Derman-Toy model.
• The tree begins with the node stating the initial interest rate. Then it connects with the other nodes with possible up and down interest rates at each interval (equal division of the total period). 

A binomial interest rate tree model suggests the two possible scenarios of a security's interest rate changes for each time interval. The first one is the upward movement (denoted as u), where the interest rate is supposed to increase, and the second is the downward movement (denoted as d), where the interest rate is assumed to fall. In a volatile financial market, the return on investment keeps fluctuating, and so do the underlying asset prices. Therefore, using the binomial interest rate tree is essential for foreseeing the chances of an interest rate rising or falling over a short period.

Some of the known properties of such a financial model are as follows:

1. The interest rates are never negative.
2. The volatility rises with the increase in interest rates.
3. The following spot rates are the multiples of e2σ.

In other words, such a model determines the possible path of the movement of the interest rate of an investment product. One of the most common pricing models, the Black-Derman-Toy model, works on this phenomenon. It is a financial tool for setting bond and derivative prices in the financial market. Although, the binomial model doesn't truly represent the real picture since it considers only two possibilities, while the interest rates may remain constant throughout the lifetime of an investment.

The binomial interest rate tree is a versatile financial model with numerous other applications, as discussed below: 

• Option Pricing: The binomial interest rate tree calculates an option's expected payoff periodically at fluctuating interest rates. It enables investors to make informed decisions about buying or selling options.
• Bond Pricing: This tool helps to determine the value of bonds that offer the benefits of the options, such as callable bonds. The model calculates the value of these options and incorporates them into the bond's price, providing a more accurate valuation.
• Risk Management: It aids in depicting the impact of changing interest rate scenarios on an investment portfolio. Risk management, thus, helps the investors identify potential risks associated with the underlying securities and take measures to mitigate them.
• Investment Decision Making: It facilitates the comparison of the potential returns of different investment opportunities under different interest rate scenarios. Investors can make investment decisions based on their risk-taking capacity and return expectations.

A binomial interest rate tree involves a series of nodes representing an underlying security's potential future interest rates. The following steps are involved in the construction of such a model:

1. Determine the period for which the tree is to be constructed. For instance, if the goal is to represent interest rates for three years, then the period would be three years.
2. Divide the period into equal intervals, such as months, quarters, or years.
3. Mark the present interest rate of the asset or security.
4. Gauge the possibility of interest rate increase or decrease, preferably the risk-neutral probability of the future interest rate. The up and down factors represent the potential changes in the interest rate at each time interval.
5. Starting with the initial interest rate, calculate the potential interest rates at each time interval and show them as nodes in a tree-like structure by connecting the nodes through lines. Each node in the tree represents a potential future interest rate at a given time.
6. Continue this process until the final time interval is reached.

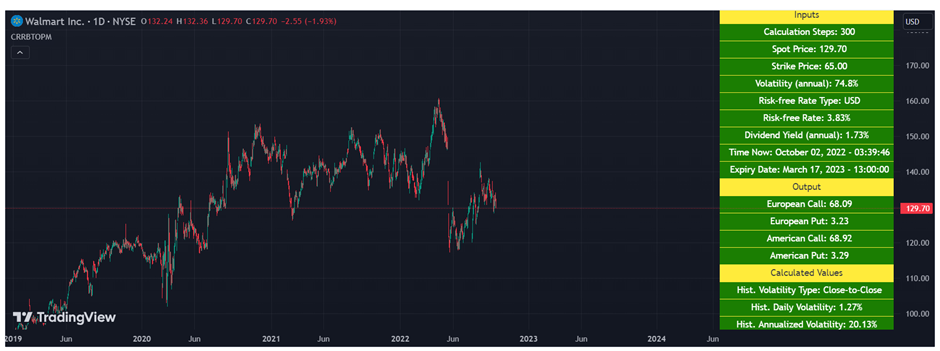
The concept is explained better using a chart from TradingView. In the chart below related to Walmart Inc., there is a numerical approach to the entire process of option valuation, even though it is very complex in nature. But it is a widely used and very useful method. Through the binomial tree, it is possible to represent diagrammatically various possible paths that the asset can see over the option’s life.

However, the price of an underlying asset will move through a random path. In each possibility, the asset price has the probability to move either up or down by any percentage. However, as the time step reduces, it becomes the same as the Black-Scholes model. Thus, the price fluctuation is factored in at every step. to show the probable paths of the asset in the tree, depicting the Binomial Option Pricing Model. This method gives the flexibility to the analyst or trader to revisit any part of the tree to find the possibility to exercise the option at the strike price before the expiry of the contract.

Source

Check out these examples for a better idea:

Example 1: Two-Period Binomial Tree

Suppose an initial investment of $1000 indicates the following information for two years:

• Upward movement factor (u) = 1.1
• Downward movement factor (d) = 0.8
• Risk-free interest rate (r) = 10%

Let us construct the binomial interest rate tree.

For year 1:

Up Interest Rate = 10% × 1.1 = 11%

Down Interest Rate = 10% × 0.8 = 8%

For year 2:

Up Interest Rate for 11% = 11% × 1.1 = 12.1%

Down Interest Rate for 11% = 11% × 0.8 = 8.8%

Up Interest Rate for 8% = 8% × 1.1 = 8.8%

Down Interest Rate for 8% = 8% × 0.8 = 6.4%

Example 2: Three-Period Binomial Interest Rate Tree

Suppose a derivative with an initial investment of $200 poses the following interest rate information for three years:

• Upward movement factor (u) = 1.2
• Downward movement factor (d) = 0.9
• Risk-free interest rate (r) = 5%

Let us show the interest rate changes over three years on a binomial interest rate tree as follows:

This has been a guide to what is Binomial Interest Rate Tree. Here, we explain the topic in detail, including its examples, uses, and how to construct it. You can learn more about it from the following articles –

• Binomial Option Pricing Model
• Call Warrant
• Binomial Distribution