Bayesian Network

Published on :

21 Aug, 2024

Blog Author :

Edited by :

Reviewed by :

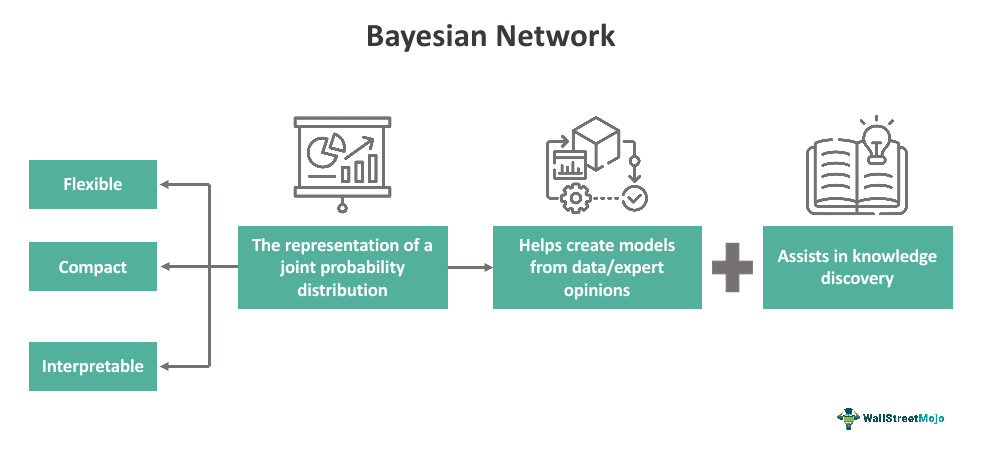
Bayesian networks refer to the flexible, interpretable, and compact representations of joint probability distributions. They can be helpful tools in knowledge discovery because directed acyclic graphs (DAG) allow for the representation of causal relationships existing between variables. Moreover, one can utilize this concept to create models from expert opinion and/or data.

Also known as belief networks, these models can help solve probabilistic problems, which depend on a lot of variables. Simply put, they can assist in predicting events and deriving connections between multiple events or variables. Such a model can be of two types – dynamic and temporal nodes. One can use it for different tasks, like anomaly detection, diagnostics, and reasoning.

Bayesian Network Definition

Bayesian network refers to a probabilistic graphical model consisting of directed edges or curves and nodes. This concept aids in knowledge discovery. It also allows individuals or organizations to develop models using data or experts’ opinions.
There are various advantages of Bayesian networks. For example, they can act as visual decision-support tools. Moreover, they can help by representing large probability distributions.
A noteworthy Bayesian network limitation is the lack of feedback loops.
This concept has applications in various areas, such as computer software and hardware, healthcare, and biology.

Bayesian Network Explained

Bayesian network meaning refers to a probabilistic graphical model representing a set or collection of variables along with their conditional dependencies utilizing DAG. It visualizes the probability of a certain domain and evaluates the probabilities for a given scenario using evidence and factual data. Moreover, it oversees the link between the various random variables in a given situation.

One can use this model in an extensive range of tasks, for example, causal modeling, anomaly detection, reasoning, and diagnostics. It is one of the most popular models utilized to reason with uncertainties concerning data.

These models comprise nodes and arcs or edges. Each of the nodes corresponds to random variables, which can be discrete or continuous. The edges or arcs represent the conditional probabilities or causal relationships between random variables. Such arcs link the nodes. Note that if there is no arc, then all nodes are independent of each other.

Let us look at a few features of such networks to understand the concept better.

It utilizes observed data to understand the system’s parameters and structures.
The model represents relationships between different variables even in an uncertain scenario.
It utilizes the network interface to compute probability.
One can use this model for different tasks, such as reasoning and anomaly detection.
It has quantitative and qualitative components. The former includes the DAG explicating the variables of interest. This is represented via nodes and the direct influences existing among them. On the other hand, the quantitative components include conditional probability distributions. These help in quantifying dependencies between variables as well as their parents in the directed acyclic graph utilizing the variables’ expansion in the conditional probability table and joint probability function.

Types

Let us look at the different types of Bayesian networks.

#1 - Dynamic

These networks model dynamic processes. They comprise a number of time slices representing the state of every variable at a specific time, t. Such a network represents the temporal assessment of a specific process and the state of every variable at distinct time intervals. In this case, edges exist between the variables from different slices, and their directions follow the direction of time, thus defining the transition network.

#2 - Temporal Event

This type of belief network comprises a number of temporal nodes. Edges connect these nodes, and every edge is a representation of a causal-temporal relation. Note that a maximum of one state exists for every variable in the temporal interest range. The value that the variable takes represents that particular interval during which the event takes place. All intervals defined for child nodes represent the potential delay between the occurrence of a parent event or the cause and its child event.

Examples

Let us look at a few Bayesian network examples to understand the concept better.

Example #1

Suppose Sam utilized the Bayesian network concept to predict the future performance of ABC stock. This approach represented the stock’s past returns along with their conditional dependencies between the future and past stock prices through a DAG. The belief network determined the stock price from the discrete stock price value set to ensure the maximization of the occurrence probability.

Example #2

Suppose XYZ Bank wanted to predict its clients’ behavior to increase its sales, evaluate risk, and create categories of its financial products efficiently. The company had limited data available. As a result, it used the Bayesian Network, which helped it create a predictive model. Based on this model, the bank created product categories and made adjustments to its existing offerings to increase its revenue.

Applications

A few real-world applications of this model are as follows:

Computer Software And Hardware: Popular organizations like Intel and Microsoft developed applications and systems utilizing this model to streamline and improve processes.
Finance And Business: The financial and business sectors are benefitting via this model, with organizations introducing software for belief networks. Banks are utilizing this model to classify loans, model, and make predictions concerning client behavior with uncertain or limited data.
Healthcare: The model’s value is impressive in the healthcare space because it solved various complicated diagnostic issues encountered earlier by this industry.
Biology: The approach has been beneficial for practitioners and researchers as they have been able to analyze gene expression data, conclude gene networking, etc.

Advantages And Disadvantages

Let us look at the benefits and limitations of belief networks.

Advantages

This model helps in parameter and structural learning.
It integrates input data from various sources for the purpose of overcoming data limitations.
The model compactly represents substantial probability distributions.
Belief models can serve as visual decision-support tools.
Another key adjective of Bayesian networks is that they transparently represent causal components between the system variables.

Disadvantages

These networks lack feedback loops.
Belief models perform continuous data representation.
Such models deal with continuous variables in a restricted manner only.
Another key Bayesian Network limitation is that creating straightforward yet expressive probability distribution is challenging.

Bayesian Network vs Neural Network vs Markov Network

The concepts of Bayesian, neural and Markov networks can seem confusing for one learning about the concepts for the first time. However, one can easily understand their meaning and purpose and avoid confusion by knowing their differences. So, let us look at their distinct features.

Bayesian Network	Neural Network	Markov Network
These probabilistic graphical models involve utilizing Bayesian inference to compute probability. Contrary to Markov networks, these utilize DAG.	This technique in artificial intelligence teaches computers to carry out data processing in a manner replicating the human brain.	This refers to an undirected graph; its links represent probabilistic dependencies that are symmetrical.
Such networks are ideal for taking events that took place and making predictions regarding the possibility that any of the various possible known reasons was the main contributing factor.	These networks help computers make decisions that are intelligent using restricted human assistance.	Markov networks simplify joint probability distributions and preserve interesting dependencies.

Frequently Asked Questions (FAQs)

1. Is Bayesian network machine learning?

Machine learning can tell how possible it is to identify a particular data pattern if a certain hypothesis is correct. On the other hand, belief models are probabilistic general models, which means one already knows something and begins with a hypothesis.

2. What is the use of a Bayesian network in machine learning?

People can utilize belief networks for an extensive range of tasks in machine learning. Examples of such tasks include multi-dimensional supervised classification, clustering, temporal modeling, and anomaly detection.

3. Are Bayesian networks still used?

Yes, one must note that belief networks are still popular. In fact, these models are still more successful compared to a deep neural network to date. Individuals or organizations use these models across different industries for prediction, modeling, and inference.

4. Why must a Bayesian network be acyclic?

It must be cyclic to guarantee that the underlying probability distribution gets normalized to one.