Bayesian Inference

Published on :

21 Aug, 2024

Blog Author :

Edited by :

Reviewed by :

Bayesian inference in mathematics is a method to determine the statistical inference to amend or update the probability of an event or a hypothesis as more information becomes available. Hence, it is also referred to as Bayesian updating and plays an important role in sequential analysis and hypothesis testing.

Also called Bayesian probability, it is based on Bayes' Theorem. Bayesian inference has many applications due to its significance in predictive analysis. It has been widely used and studied in science, mathematics, economics, philosophy, etc. Its potential in data science looks especially promising for machine learning.

What is Bayesian Inference?

Bayesian inference is a mathematical technique to accommodate new information (evidence) to existing data. Thus, its importance can be associated with the constant requirement to keep data updated and hence, useful.
Bayesian updating has its base in Bayes' Theorem. Using the formula, the probability of the actual event by considering the new changes can be found easily.
It is but one technique in statistical inference. Frequentist probability is another method that determines the probability based on the repetitive data set.

Bayesian Inference Explained

Bayesian inference in statistical analysis can be understood by first studying statistical inference. Statistical inference is a technique used to determine the characteristics of the probability distribution and, thus, the population itself. Therefore, Bayesian updating helps to update the characteristics of the population as new evidence comes up. Hence, its role is justified, as new information is necessary to obtain accurate results.

Now, let's systematically understand the technical aspect of a Bayesian inference model.

Bayes' theorem states that,

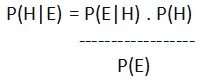
Here, H is the hypothesis or event whose probability was determined.

E is the evidence or the new data that can affect the hypothesis.
P(H) is the prior probability or the probability of the hypothesis before the new data was available.
P(E) is the marginal likelihood and probability of the event occurring.
P(E|H) is the probability that event E occurs, given that event H has already occurred. It is also called the likelihood.
P(H|E) is the posterior probability and determines the probability of event H when event E has occurred. Hence, event E is the update required.

Thus, the posterior probability increases with the likelihood and prior probability, while it decreases with the marginal likelihood.

Applications

Bayesian inference network has many applications. For example, it is used for statistical data analysis, to find the probability, and make predictive analysis. Here are a few of the prominent uses:

The increasing use of the Bayesian inference model in machine learning looks promising. For example, it is used to develop algorithms for pattern recognition, e-mail spam filtering, etc.
Bioinformatics and its applications in healthcare are very significant, especially in the general cancer risk model and continuous individualized risk index.
Jurors use Bayesian probability to find the likelihood of a particular case as new evidence accumulates.
It is also used in research to find the probability of an event when new observations become available.
Finally, Bayesian updating is prominent in finance, trading, marketing, and economics. It depends on the individual who uses this technique to get the maximum benefits.

Examples

Let's discuss a few examples of Bayesian inference in statistical analysis.

Example #1

The following table gives information about four groups of people based on two characters – speaking English and reading the newspaper.

Observations	Speaks English (E)	Doesn't speak English (E')	SUM
Reads newspaper (N)	20	30	50
Doesn't read the newspaper (N')	25	15	40
SUM	45	45	90

Event E refers to the number of people speaking English.

Event E' is the logical negation of E and refers to people who do not speak English.

Similarly, event N refers to the number of people who read the newspaper

Event N' refers to the number of people who do not read the newspaper

Thus, P(E) + P(E’) = 1

Since the total probability is always equal to one, people can speak English.

Similarly, P(N) + P(N’) = 1

The population size is 90.

So let's calculate the probability of N given E, i.e., P(N|E).

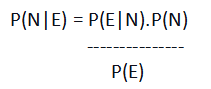
P(N) = 50/ 90

P(E) = 45/ 90

P(E|N) = 20/ 50

Thus, P(N|E) = / (45/ 90)

= 20/ 45

But this can also be inferred directly from the table (without using the formula).

Observations	Speaks English (E)	Doesn't speak English (E')	SUM
Reads newspaper (N)	30	30	60
Doesn't read the newspaper (N')	25	15	40
SUM	55	45	100

Now, suppose the number of people who speak English and read newspapers increases to 30.

P(N) = 60/ 100

P(E) = 55/ 100

P(E|N) = 30/ 60

Thus, P(N|E) = / (55/ 100)

= 30/ 55

Example #2

Metanomic is a software company that supports game developers by simulating game economies, and it is playing a significant role in building the Metaverse. Recently, Metanomic acquired Intoolab, an artificial intelligence-powered biomedicine platform. Intoolab was the first to develop a Bayesian network AI engine.

The acquisition will help the parties realize the vast potential of statistical techniques like Bayesian inference and create better user experiences for the players. In addition, the Intoolab technology will be a great addition to Metanomic as it brings together players from around the world in real-time.

Bayesian Inference vs Maximum Likelihood vs Frequentist

Like Bayesian inference, maximum likelihood and frequentism are important concepts in statistical inference. However, their approach and scope are different.

As the name suggests, maximum likelihood refers to the condition where the probability that an event will occur is the highest. In statistics, this is arrived at by estimating the observed value (parameters).
Based on certain data, a scientist determines that the probability of a particular outcome is 65%. But they want to estimate when the event becomes 100% probable. So they try changing the data to attain the maximum probability through simple trial and error.
Frequentist probability, or frequentism, determines the likelihood of an event by considering the frequency of a particular observation, i.e., how many times a particular data is observed. Frequentism and Bayesian inference are often considered rival approaches.
For example, the probability of getting heads when a coin is tossed is 50%. A Bayesian would say it's because there are only two possibilities – a head and a tail. And the probability of any of these appearing is the same. However, a frequentist would claim that the probability is 50% because if the coins were tossed an adequate number of times, heads appeared half the time.
All these concepts have significant applications in highly data-driven fields like research, machine learning, business, etc.

Frequently Asked Questions (FAQs)

1. Is Bayesian inference machine learning?

No. Bayesian inference cannot be correlated to machine learning. It can be a common confusion as it has a very important role in artificial intelligence. Machine learning is only one of the many applications of Bayesian probability.

2. How does Bayesian inference work?

Bayesian probability accommodates new evidence or data to determine the probability of an event whose likelihood was already estimated. It is necessary that as new information becomes available, the systems dependent on the data, too, change. This can be extremely helpful in the long run and avoids stagnation in a system by providing room for growth.

3. How do you do Bayesian inference?

Bayesian inference network is based on Bayes' theorem.
P(H|E) = P(E|H) . P(H)
------------------
P(E)
P(H) is the probability of the event, which was calculated earlier.
P(E) is the probability of the new information being made available recently.
P(E|H) is the probability of the new information provided that the earlier event has already occurred.
P(H|E) is what is to be found, and it determines the probability of the earlier event by accommodating the new information.