Arrow's Impossibility Theorem

Published on :

21 Aug, 2024

Blog Author :

N/A

Edited by :

prarthana Khot

Reviewed by :

Dheeraj Vaidya

What Is Arrow's Impossibility Theorem? 

Arrow's Impossibility Theorem says that in a fair ranked-voting system of elections, individuals' order of preference of alternatives cannot determine the transparent pan-community-ranked preferences. This theorem helps to bring out the gap in the modern & prevalent ranked system of voting embedded in the paradox of social choice.

Arrow's Impossibility Theorem

This theorem is a part of Arrow's social choice theory 'based on the representation of a society's preference concerning individuals' preferences. The consequences of Arrow's Impossibility Theorem are quite important for many democratic processes like elections. But unfortunately, it also demonstrates that none of the voting systems in the world is flawless. As a result, it is impossible to obtain a realistic result ever.

Table of contents
  • As per Arrow's impossibility theorem, there is a very least chance of devising a voting system where an individual's preferred choice would represent' society's preference.
  • It highlights that one cannot determine a clear preference order after following the necessary principles of fair voting procedures.
  • If the election has to be fair and just, then the five conditions must be met: no dictatorship, Pareto efficiency, Independence of irrelevant alternative, unrestricted domain, and social ordering. 
  • Moreover, this theorem can identify the shortcomings of any voting system.

Arrow's Impossibility Theorem Explained 

Arrow's impossibility theorem states that the social welfare function assigns a social preference of order to every valid profile of individual choice of arrangements of a given set of options. The construction of social welfare, which reflects the preference of all individuals constituting a society, is an impossible task. So, it states that it is very difficult to set up reasonable democratic procedures for aggregating individual preferences into a social preference for making social change.

Arrow's impossibility theorem is also called Arrow's theory of social choice or general impossibility theorem. The theorem is named after the economics Nobel prize winner – Economist Kenneth Arrow. He proposed it in 1951 in a paper, which then turned into a book called Social Choice and Individual Values. The book explains the effect of individual choices on society during elections or voting.

This theorem begins by setting up a reasonable criterion for voting conditions to accumulate the preferences of all the individuals to represent society's preferences. However, the said conditions can either lead to irrational team decisions or, straightforwardly, an undemocratic judgment. Therefore, sometimes in the arrow impossibility theorem welfare economics and Arrow's impossibility theorem economics discussion, it is also called the dictator theorem. 

In this theorem, transitive means a sensible arrangement, and intransitive means insensible order. For example, if one likes apples the most, then like oranges and bananas the least. As a result, this order is transitive. However, when purring the preference of the three fruits in best to least arrangements, one gets the following: one prefers apples to oranges, oranges to bananas, and bananas to apples, which is called intransitive.

Arrow's Impossibility Theorem's Five Criteria

Arrow tried to create a system of preference for voting that would be just, consistent, and more transitive in nature of group preference. Arrow devised five criteria to make the voting fair for the same to happen. They are the following: 

  1. Non-dictatorship
  2. Independence of irrelevant alternatives
  3. Pareto efficiency
  4. Unrestricted domain & 
  5. Social ordering

As per the theorem, it is impossible to violate the five criteria mentioned here and lead to intransitive voting or cyclic preferences. The country's elected leader can even be a 50% vote winner. As an Arrow's Impossibility Theorem proof, one can study the US presidential elections of 1992, in which Bill Clinton won the elections with just 43%  of the popular votes. Despite his rivals – George W bush got 38%  votes, and Ross Perot got 19% votes.

Conditions In Arrow's Impossibility Theorem

There are certain criteria for the applicability of Arrows impossibility theorem. Only then can a country hold fair and reasonable elections. Each one of these conditions is vital for electoral procedures. They include the following:

#1 - Non-Dictatorship 

It states that a voter's choice of a candidate can not be the choice of every member of the society, and his preference cannot represent the society. Hence, one must consider every member of society's preferences to comply with the social welfare function.

#2 - Independence Of Irrelevant Alternative

The social ranking of a particular subset must be independent of the change in the ranking of petty alternatives of that subset by an individual of the society.

#3 - Pareto Efficiency

Society should appreciate the concordant preferences made by every single person. It means that if the majority of the individuals in the society select an option, it must comply with the order of social preference. Moreover, the voting outcome should be devoid of any empathetic attitude towards the preference profile.

#4 - Unrestricted Domain

Under this condition, one should count the choices of all the voters so that it represents a full ranking of social preference.

#5 - Social Ordering

This condition requires that voters be able to exercise their choices of the vote in a manner that is inter-related and in order from best to worse.

Example 

One needs to study the Arrow's Impossibility Theorem example, as discussed here, to understand the theorem. 

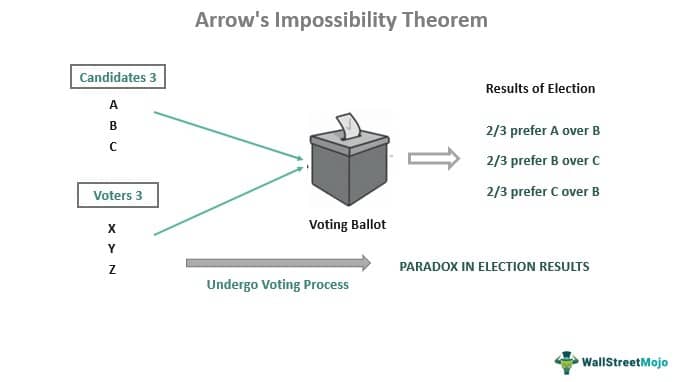
Let us assume there are three different varieties – A, B & C of coffee- at Starbucks. A group of 3 people is selected to convey their order of preference for the varieties of coffee at Starbuck, namely – David, Diana & Brian. These people must disclose their choice along with the coffee varieties' ranking. So, they can rank their choices according to their taste, from best to worse. 

After a while, David, Diana & Brian present their order of preference as below:

David - ABC

Diana - BCA

Brian- CAB

One can explain the result as below:

David prefers A over B and B over C. Diana prefers B over C and C over A. Brian prefers C over A and A over B. So, one can conclude that 1/3 prefers A>B>C, 1/3 prefers B>C>A, and 1/3 prefers C>A>B.

In other words, 

2/3 prefer A over B 

2/3 prefer B over C; and

2/3 prefer C over A

Therefore, a paradox occurs where 2/3 of each of the majority prefers A over B, B over C, and C over A. Thus Kenneth Arrow's impossibility theorem gets validated as one of the conditions in the theorem is violated while ranking the order of preference amongst the three alternatives A, B & C.

Frequently Asked Questions (FAQs)

Why is Arrow's Impossibility Theorem important?

Arrow's impossibility theorem is important regarding the consequences it has on the democratic elections for choosing government through voting. The theorem promulgates that a transparent pan- community-based ranked system of voting preferences is not known through transforming a person's choice using a just ranked- voting system of elections.

What are Arrow's Impossibility Theorem requirements for a social welfare function?

For satisfying a social welfare function, Arrow made the following set of requirements mandatory:
Weak Pareto – it means that society follows the decision of choosing the preference that everyone in the society has chosen.
Binary Independence of irrelevant alternatives- an individual's preference for a pair of options controls society's preference regarding that pair of options.
Non-dictatorship – every individual’s preference is not respected every time.

How can Arrow’s Impossibility Theorem affect the political process?

As Arrow’s impossibility theorem is a theorem in social choice. It states the impossibility of observing an ideal voting system. It also states that the results cannot reflect voters' choices even if they follow fair voting procedures.

What is the difference between the voting paradox and the Arrow’s Impossibility Theorem?

According to the voting paradox, on the political ground, the voting outcomes will generally reflect the majority preferences at large. However, Arrow’s impossibility theorem states the opposite. It states that if one follows fair voting principles, the results do not usually reflect voters' preferences.

This article has been a Guide to what is Arrow's Impossibility Theorem. We explain its meaning, conditions, criteria along with an example. You can learn more about finance from the following articles –