Arc Elasticity

Published on :

21 Aug, 2024

Blog Author :

Edited by :

Reviewed by :

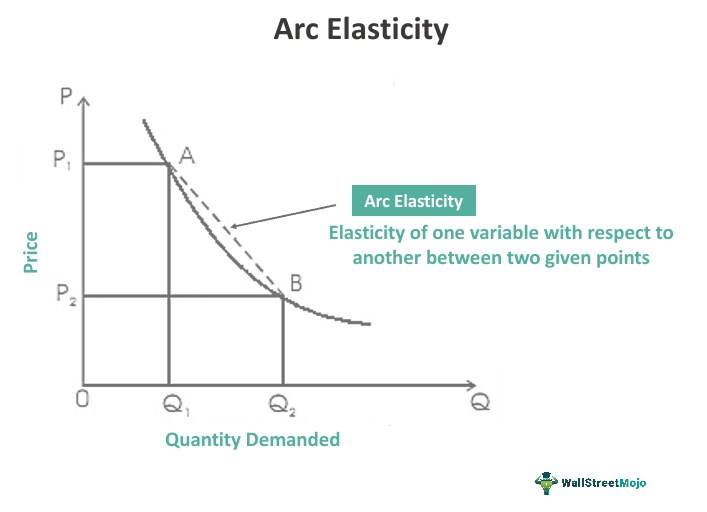
Arc elasticity is a concept used to evaluate the responsiveness of supply or demand to changes in price across a specific price range. Its primary objective is to gauge the sensitivity of producers or consumers to price fluctuations. Moreover, traders utilize the price elasticity of supply or demand to gain valuable insights for informed trading decisions.

It finds wider use in economics for determining the impacts of price variation on market behavior like producer profitability and demand patterns. Higher arc elasticity means huge shifts in demand or supply due to little price changes representing a more responsive market and vice versa. It helps policymakers, businesses, and economists with market dynamics forecasts for formulating impactful pricing strategies. It can capture the variation of elasticity at different price ranges.

What Is Arc Elasticity?

Arc elasticity is a method used to analyze how supply or demand responds to changes in price over a specific range.
Its primary objective is to understand the degree of sensitivity that producers or consumers exhibit toward price variations.
For traders, it helps assess the level of price elasticity for supply and demand, offering valuable insights for decision-making in trading activities.
It gets determined by dividing the percentage change in quantity by the percentage change in price, using the formula (∆Q/Q) / (∆P/P), where ∆Q represents the change in quantity, Q is the initial quantity, ∆P indicates the price change, and P represents the initial price.

Arc Elasticity Explained

Arc elasticity is a beneficial measure for assessing the elasticity of supply and demand between two points on a curve providing deep insights into the responsiveness of price or demand over a price range. Its determination involves using a midpoint between the initial and fresh rice plus quantity values, giving way to a more accurate depiction of elasticity on the whole.

Its implication becomes significant as:

Any value of more than one implies elastic supply or demand representing highly responsive quantity towards price changes.
Any value less than one implies inelasticity in supply or demand, representing less responsive quantity towards price changes.
Any value equal to one shows unitary elasticity where percentage changes in quantity and price are proportional.

Furthermore, its drawback lies in not providing precise elasticity value at any given price point. Additionally, it has applications in the following field;

Investors of securities use it to gauge market outcomes due to price changes.
Policymakers take its help to assess the effect of pricing policies.
Mathematicians use it in mathematical modeling and optimization.

Formula

Arc elasticity gets calculated by dividing the percentage change in quantity by the percentage change in price. The arc elasticity equation can be expressed as follows:

Arc Elasticity = (∆Q/Q) / (∆P/P)

Where:

∆Q = the change in quantity demanded,
Q = the initial quantity,
∆P = the change in price, and
P = the initial price.

The above formula could be used to:

Make right decisions
Predict market behavior
Formulate effective strategies for navigation across a complex financial landscape.
Policymakers take its help to the evaluation of the efficiency of pricing policies.
Aids in market efficiency
Encourage innovation
Foster market competition

Additionally, the arc elasticity of the supply formula:

Arc Elasticity of Supply = (∆Qs/Qavg) / (∆P/Pavg)

Where:

∆Qs = the change in quantity supplied,
Qavg = average of the initial and new quantities supplied,
∆P = change in price, and
Pavg = average of the initial and new prices.

Examples

Let us use a few examples to explain the topic.

Example #1

Given:

Initial quantity (Q1) = 100 units

Final quantity (Q2) = 80 units

Initial price (P1) = $10

Final price (P2) = $12

To calculate the arc elasticity of demand, we use the formula:

Arc Elasticity = (∆Q/Q) / (∆P/P)

∆Q = Q2 - Q1

= 80 units - 100 units

= -20 units

∆P = P2 - P1

= $12 - $10

= $2

Substituting these values into the formula, we have:

Arc Elasticity = ((-20 units / 100 units) / ($2 / $10))

= (-0.2) / (0.2)

= -1

A unitary elastic demand means that a 1% increase in price results in a 1% decrease in quantity demanded. In this case, the elasticity value of -1 indicates that a 1% increase in price leads to a 1% decrease in quantity demanded.

Example #2

Consider Customer A, a regular purchaser of Product A from Company A in the U.S. Initially, when the price is set at $50, Customer A buys 100 units. However, Company A decides to raise the price to $60 over time, resulting in Customer A decreasing their purchase quantity to 80 units.

This situation demonstrates that as the price of Product A increases, Customer A adjusts its demand accordingly. The price change from $50 to $60 represents a 20% increase, while the decrease in quantity demanded from 100 units to 80 units reflects a 20% decrease.

Analyzing the arc elasticity allows us to determine the responsiveness of Customer A to the price alteration of Product A. When the percentage change in quantity demanded equals that of the percentage change in price, which in this case is 20%, the arc elasticity becomes -1. Thus, we find that the demand is unitary elastic, adjusting proportionally to price fluctuations.

Moreover, understanding the arc elasticity helps Company A evaluate how sensitive Customer A is to product price variations. This knowledge can enable Company A to meet customer demands in the competitive US market efficiently.

Arc Elasticity vs Point Elasticity

The differences between the two can be studied through the table below:

Arc Elasticity	Point Elasticity
Encompasses changes over a particular price ranges	Helps in the analysis of elasticity at a particular price point
Evaluates the level of response of demand or supply over a range	Assesses the responsiveness of supply or demand at a single point
Acts as a more accurate metric of elasticity	Provides simple approximate values of elasticity
Aids price changes that happen spread across a certain range	Comes to aid while examining elasticity at certain price levels
Needs data for both final and initial prices and quantities	Asks for data for a single price point quantity
More sensitivity towards quantity and price changes	Little sensitivity to quantity change and price changes

The above differences help policymakers, elasticity, businesses, and economists choose the right metric based on the particular context & research objectives.

Frequently Asked Questions (FAQs)

1. Is midpoint elasticity and arc elasticity the same?

No, midpoint elasticity and arc elasticity are not the same. They are two different measures of price elasticity of demand. Midpoint elasticity is a measure of price elasticity that calculates the percentage change in quantity demanded divided by the percentage change in price using the midpoint formula. It considers the starting and ending values of both price and quantity to calculate the elasticity. On the other hand, arc elasticity is another measure of price elasticity that calculates the percentage change in quantity demanded divided by the percentage change in price, using the average values of price and quantity. It considers the average price and quantity between two points to calculate the elasticity.

2. What are the advantages of arc elasticity of demand?

It provides a more balanced view of elasticity by capturing the effects of price changes regardless of their direction. Arc elasticity can handle situations where the demand curve is not linear. It accommodates changes in both price and quantity over a range of values, making it useful when analyzing elasticities for curved demand functions.

3. What are the applications of arc elasticity?

Arc elasticity finds applications in various areas, including:
a. Pricing decisions
b. Tax incidence analysis
c. Demand forecasting
d. Market analysis