Table Of Contents
Annuity Factor Meaning
The annuity factor is a mathematical concept that helps find the present value of a future deposit or withdrawal. It is used in finance and helps calculate the maximum amount of money that can be withdrawn from a retirement account without penalties. The concept also applies to capital budgeting.
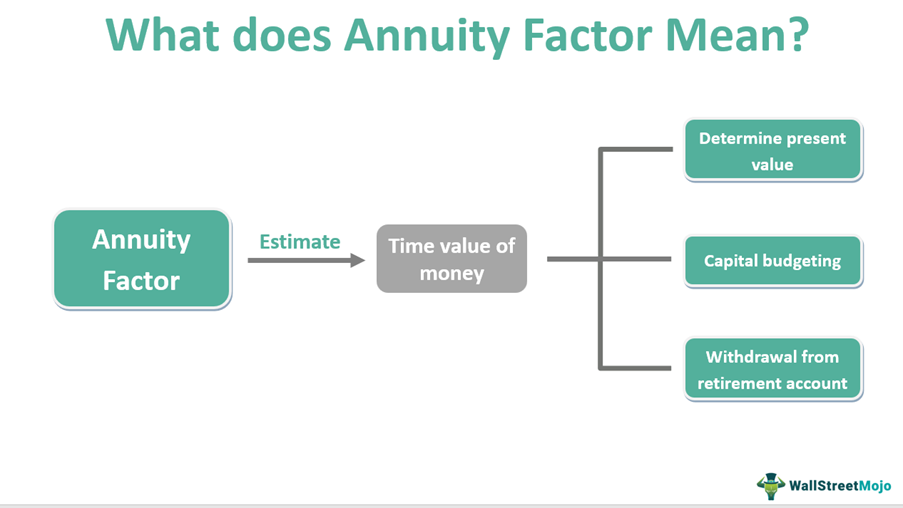
As the name suggests, its use can be extended to any annuity. Annuity refers to any financial instrument that has steady cash outflows. In such cases, it helps determine the time value of money. Another application is calculating equated loan installments. Thus, the annuity factor helps in decision-making.
Table of contents
- The annuity factor refers to a mathematical figure that helps determine the present economic worth of any future financial instrument.
- This helps make estimations like how much money can be withdrawn from a retirement account so that recouping the value at a future date without penalties will be possible.
- The computation of the maximum withdrawal from individual retirement accounts follows the Internal Revenue Service (IRS) guidelines and specifications.
- The valuation factor depends mainly on the period of deposit/ investment and interest rates. Further, the present value also depends on the cash outflow or income from the instrument.
Annuity Factor Explained
The annuity factor requires a thorough understanding of some other preliminary concepts. So let's start by understanding the term 'annuity'. An annuity is a financial instrument that earns a regular income. It can be interest payments, pensions, or regular insurance disbursements.
The factor is a specific mathematical value that one can use to find the present value of payments. For example, what will be the present value of a 12% bond that will mature in three years? The annuity factor helps to answer this question. Other methods, like fixed amortization, discounted payback, net present value, etc., can help with similar calculations.
But the use of the factor can be seen more frequently in IRA. Individual retirement accounts (IRAs) help people make early savings for post-retirement. Since it is primarily meant for savings, making withdrawals from the account might not be a great idea. However, there are some limitations to this. For example, if an individual makes withdrawals before they are 59 ½ years of age, they incur a 10% penalty.
Nevertheless, some exceptions exist – educational expenses, first-time home purchases, etc. Also, a Roth IRA can have an advantage in this case. However, the point here is that a person cannot keep withdrawing from their IRA. Beyond a limit, they will incur a penalty. This limit can be determined using the annuity factor method.
The IRS recommends a set of annuity factor tables for the valuation of withdrawals, payments, deposits, etc. It uses life expectancy data to determine the evaluation. Using this, an individual can make maximum drawings depending on their present value. The actuarial table published by the IRS provides the valuation factor for annuities, life estates, etc. The valuation factors for different specifications (annuities paid at the end/ beginning of the year) vary and are mentioned clearly by the IRS.
Formula
There are two methods to calculate the annuity factor. The methods are similar but have slight variations.
Method 1
Annuity factor, AF =
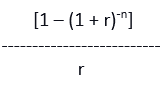
Here, 'n' is the number of years, and 'r' is the interest rate
Method 2
The annuity factor can also be calculated as the sum of individual discount factors.
The discount factor for year 1: (1 + r)-1
The discount factor for year 2: (1 + r)-2
And so on.
The net present value of an annuity can be calculated as the product of the outflow during a year/ period and the annuity factor.
Calculation Example
Let's work out a calculation to understand the net present value of the annuity.
Cash outflow from year 1 = $100,000
Cash outflow from year 2 = $120,000
Investment period = 2 years
Interest rate = 6%
Following the steps will help in the more straightforward calculation:
Step 1: First, calculate the factor using the above formula.
Step 2: The easier method would be to calculate (1 + r). Here, the value would be 1.06.
Step 3: Now, square the value (1 + r) since n=2.
(1 + r)2 = 1.1236
Step 4: Next, take the reciprocal of this value, as (1 + r) is raised to a negative power.
1/ (1 + r) = 0.8899
Step 5: Subtract this value from 1.
1 – 0.8899 = 0.11
Step 6: Divide 0.11 by the interest rate, i.e., 0.06.
The annuity factor will be 1.8333.
Step 7: The present value can be calculated as the product of cash flow and the factor.
So, the present value of Year 1 = (1.8333 x 100,000) = $183,330
The present value of Year 2 = (1.8333 x 120,000) = $219,996
An alternate method to find the annuity factor as the sum of discount factors:
AF = DF1 + DF2 + … + DFn
Here, n = 2 and r = 6%
DF1 = (1 + 0.6)-1
DF2 = (1 + 0.6)-2
AF = 0.9434 + 0.8900
= 1.8333
Frequently Asked Questions (FAQs)
The formula to find the factor is as follows: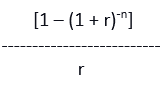
Here, 'r' is the interest rate and 'n' is the number of years.
The IRS annuity factor table can be used to ascertain the value of an annuity for different scenarios. The value can be used directly for valuation purposes, as it considers life expectancy data for estimation.
The present value annuity factor helps find the present value of future investments or deposits. Because of this, it plays an important role in trading and capital budgeting and also helps determine the maximum withdrawal that can be made from a retirement account.
The annuity factor is the sum of all discount factors for each year. The discount factor can be calculated as (1+r)-n, where n = 1, 2, 3, …
Recommended Articles
This article has been a guide to what is Annuity Factor. Here, we explain it in detail with its formula, calculation, and example. You may also find some useful articles here -
