Amortized Loan Formula

What is Amortized Loan Formula?

The amortized loan formula deals with the determination of annual or monthly payment that the borrower has to make to the lender for the loan undertaken by them. The Annual payment is composed of annual interest payments and the annual portion of the long-term debt. The interest component in the annual payment remains to be high during the initial tenure of the loan, however, during the ending tenure, the principal components dominate the annual payment.

The annual payments could be determined using the present value of the annuity formula. The amortized payment depends upon the rate of interest, tenure of the loan, borrowed sum, and the nature of compounding as per agreement between the lenders and the borrowers. The amortized payment is determined to let the lender anticipate how much it would get through the lend sum to be serviced by the borrower.

The formula is expressed as follows: –

Here,

• The rate of interest is represented as i.
• The tenure of the loan is represented as n.

Explanation

The amortized loan can be calculated by using the following steps:

Step 1: Firstly, the borrower has to determine the loan amount. The borrower citing his capacity and with the availability of loan, calculators determine the loan amount which they desire so that they can fill up the shortfall of funds.

Step 2: Next, determine the rate of interest that the lender would be most likely to lend the amount. Basis the conditions of the economy, and as per the expectations of lenders, there could be a specific range of interest rates available to the borrowers. The borrowers have to choose the best rate of interest from the available options.

Step 3: Next, determine the tenure of the loan, which the borrower believes he or she could service basis the paying capacity of the borrower.

Step 4: Next, determine the product of the borrowed sum, rate of interest, and with the sum of unity and rate of interest having the power of tenure of the loan.

Step 5: Next, deduct the sum of unity and rate of interest having the power of tenure of the loan and the unity.

Step 6: Next, divide the resulting value from step 4 with the resulting value of step 5 to arrive at the amortized loan amount to be serviced by the borrower that the borrower has to pay to the lender to amortize the loan.

Examples of Amortized Loan Formula

Example #1

Let us take the example of a borrower who is looking for finance for his new home. There is one lender who wishes to lend a loan of $2 million with a rate of interest of 8 percent for the tenure of 20 years. Help the borrower determine the monthly amortized loan amount.

Use the following data for the calculation of Amortized Loan Amount

Calculation of monthly amortized loan is as follows –

• =[$2,000,000 x 0.08 / 12 x (1+0.08 /12) ^12×20] / [(1+0.08/12) ^12×20 – 1)
• = [$65,690.70] / [3.926802771]

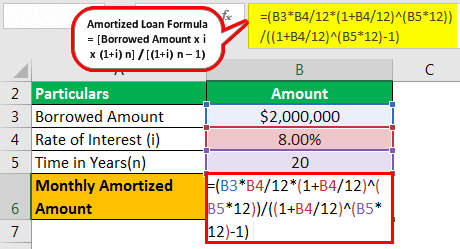
Monthly Amortized Loan Amount will be –

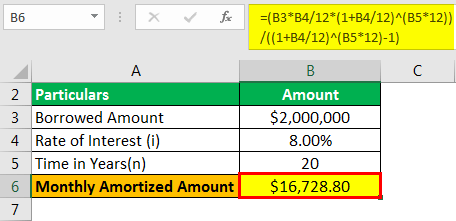
• Monthly Amortized Amount = $16,728.80

If the borrower undertakes the loan, then he has to service a monthly amortized amount of $16,728.80 for the period of 20 years.

Example #2

Let us take the example of a borrower who is looking for finance for his new car. There is one lender who wishes to lend a loan of $0.5 million with a rate of interest of 8 percent for the tenure of 5 years. Help the borrower determine the monthly amortized loan amount. Determine the monthly amortized amount as displayed: –

Use the following data for the calculation of Amortized Loan Amount

The calculation of monthly amortized loan is as follows –

• = [$500,000 x 0.08 / 12 x (1+0.08 /12) ^12×5] / [(1+0.08/12) ^12×5 – 1)
• = [$4,966.15] / [0.489845708]

Monthly Amortized Loan Amount will be –

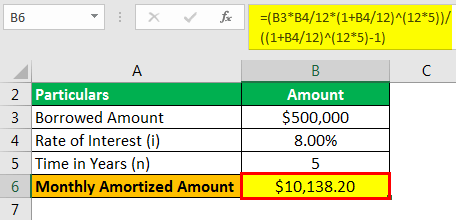
• Monthly Amortized Amount = $ 10,138.20

If the borrower undertakes the loan, then he has to service a monthly amortized amount of $ 10,138.20 for five years.

Relevance and Use

To successfully service the loan, the borrower has to determine the amortized loan amount that he has to service throughout the tenure of the loan. Amortized Loan is considered to be advantageous if the borrower makes early payments at critical junctures to reduce the principal balance, which would, in turn, lower the high-interest payments. Before taking additional debt, it is advisable to assess the existing open accounts of loans to avoid the situation of a debt trap.

The amortized loan amount should be at least 35 percent of the annual or monthly income. Whenever the rate of interest falls, always maintain the same value of amortized amount and reduce the tenure of the loan. This would ensure faster servicing of loans within the allocated time frame.

Amortized Loan Formula in Excel

Now, let us take the excel example to illustrate the concept of the amortized loan in the excel template below. The PMT function is the finance function of the excel, which helps in the determination of an amortized loan amount. The syntax of pmt is represented as follows: –

=pmt (rate, nper, pv, [fv], [type])

Here,

• The rate of interest is represented as a rate.
• The number of periods is represented as nper.
• The loan amount is represented as the pv.
• The future value is represented as fv.
• The pmt value to be determined at the or beginning of the period is represented by type.

Let us consider the examples in the excel to further illustrate the concept of an amortized loan.

Example #1

Use the following data for the calculation of the Amortized Loan Amount in excel.

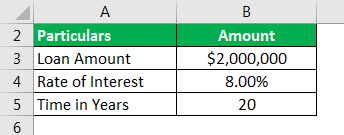
Calculation of Monthly Payment using the PMT function is as follows,

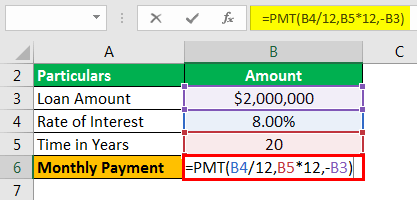
• =PMT(8.00%/12,20*12,-$2000000)

Monthly Payment will be –

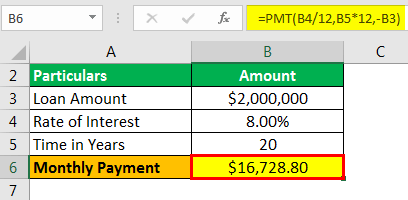
• Monthly Payment = $16,728.80

Similarly, let us consider the example 2 in the excel to further illustrate the concept of amortized loan. The table provides a detailed explanation of the risk premium.

Example #2

Use the following data for the calculation of the Amortized Loan Amount in excel.

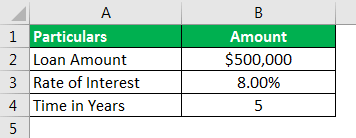
Calculation of Monthly Payment using the PMT function is as follows,

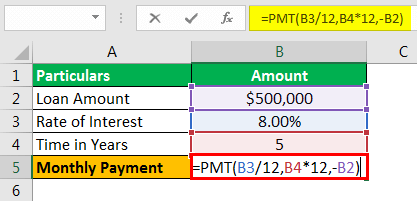
• =PMT(8.00%/12,5*12,-$500000)

Monthly Payment will be –

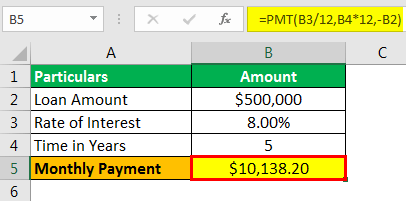
• Monthly Payment =$10138.30

Recommended Articles

This has been a guide to the Amortized Loan Formula. Here we discuss the formula for calculation of Amortized Loan along with practical examples and a downloadable excel template. You can learn more about financial analysis from the following articles –

• Exchange Rate Formula?
• Calculator for Loan Repayment
• Loan Calculator
• Principal Amount of Loan