Akaike Information Criterion

Published on :

21 Aug, 2024

Blog Author :

Edited by :

Reviewed by :

The Akaike Information Criterion (AIC) is a method used to evaluate how well different models fit a given dataset. It serves as a prediction error estimator, considering the model's quality and relative performance.

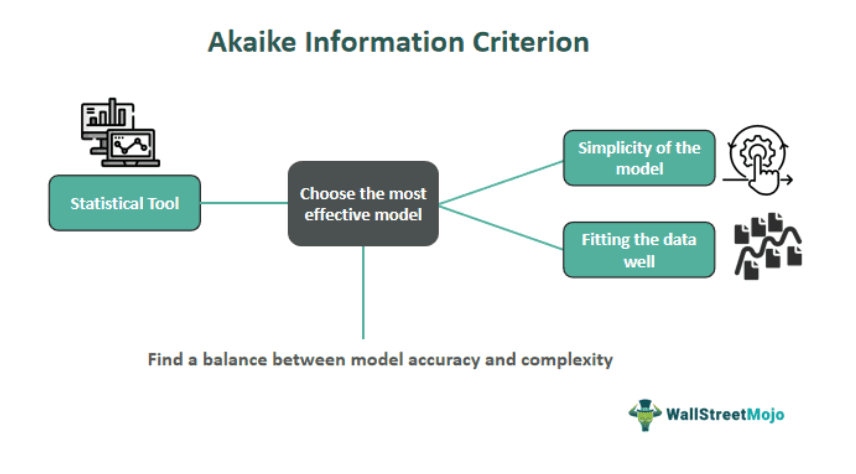
AIC produces a numerical value known as the AIC score, which helps determine the most suitable machine learning model for a specific dataset, accounting for challenging testing conditions. A lower score indicates better performance. This approach is particularly useful for small datasets or time series analyses. Introduced by Japanese statistician Hirotugu Akaike in the early 1970s, AIC ranks models based on their ability to fit data under varying conditions.

What Is the Akaike Information Criterion (AIC)?

The Akaike information criterion is a model-testing technique that ranks models based on their ability to fit a specific dataset.
The statistical technique was developed in the early 1970s by a Japanese statistician, Hirotugu Akaike, and hence is named after him.
The method results in an AIC score for every model and is compared; the lower AIC score is preferred.
It is also observed as an error prediction estimator and a means of testing the fitness and quality of different models.

Akaike Information Criterion Explained

The Akaike Information Criterion tests models based on their ability to fit datasets according to parameters and data size, estimating prediction error. Introduced by Hirotugu Akaike in the 1970s, it serves as a way to rank models and guide researchers in selecting the appropriate model for their study.

AIC assists researchers in choosing the right model, especially when dealing with multiple parameters and varying data sizes. It utilizes a formula incorporating the logarithm of the model's likelihood and quality. Although other methods exist, AIC remains popular for deducing the most suitable model.

The interpretation of AIC is based on its score, calculated by software. When comparing multiple models, each is assigned an AIC score, with a lower score indicating a better fit. AIC scores may have a log scale component, allowing for negative values, but researchers typically choose the model with the smallest AIC score.

Formula

The AIC value of a model is calculated using the following formula:

Examples

Here are some examples of Akaike information criteria:

Example #1

In finance, the Akaike Information Criterion (AIC) plays a role in model selection for predicting stock prices. Suppose a financial analyst evaluates different time series models to forecast stock returns. By employing AIC, the analyst can compare complex models with different lag orders, such as autoregressive integrated moving average (ARIMA) models.

The AIC allows the analyst to strike a balance between model accuracy and simplicity, helping choose the optimal model that captures the underlying patterns in stock price movements while avoiding overfitting, ultimately enhancing the precision of stock return predictions.

Example #2

Consider an economist examining competing models to explain inflation rates in a given country. Factors such as interest rates, money supply, and gross domestic product (GDP) growth could influence inflation. By applying the Akaike Information Criterion (AIC), the economist can systematically compare different combinations of explanatory variables and model structures.

The AIC aids in identifying the model that best balances explanatory power and model simplicity, helping economists discern the key drivers of inflation. This application of AIC ensures that the chosen model effectively captures the economic dynamics without unnecessary complexity, facilitating more accurate analyses and predictions of inflationary trends.

Example #3

Another example is the practical application of the Akaike Information Criterion (AIC) in optimizing spatial econometric models, specifically in determining the optimal number of k-nearest neighbors (knn) for the spatial weight matrix (W). Certain studies employ AIC to evaluate and compare non-nested spatial models with varying knn when faced with geolocated point data exhibiting diverse spatial patterns.

By minimizing AIC across competing models, the approach identifies the ideal knn, ensuring the best fit for the model. The recommendation is to estimate spatial models within a specified knn range, such as 2 to 50 or 100, and choose the model with the lowest AIC, underscoring this method's simplicity, universality, and robustness across different spatial patterns.

Example #4

Suppose we have a linear regression model with two parameters (k = 2), and the maximized likelihood function is 0.05. The calculation would be as follows:

AIC = 2*2 -2*ln(0.05)

Assuming ln(0.05) is approximately -2.9957 (for simplicity), the AIC would be

AIC≈4−2×(−2.9957)

AIC≈9.9914

So, in this example, we calculated an AIC value of approximately 9.9914 for a specific linear regression model; the assessment would involve comparing this AIC value with those of alternative models. If, for instance, another linear regression model with a different set of parameters or features yields an AIC value of, let's say, 12.5. The model with the lower AIC value (9.9914) is considered preferable.

Advantages And Disadvantages

Some of the important advantages and disadvantages are the following:

Advantages

AIC aids in identifying the most suitable model for a given dataset based on its fitness.
Enables comparing multiple models using AIC scores, assisting in model selection.
The AIC serves as an estimator of prediction error, enhancing the understanding of model performance.
The process is largely automated and can be efficiently performed by software, reducing manual effort.
AIC techniques contribute to deriving the quality of models, aiding in evaluating their effectiveness.

Disadvantages

In situations with limited data, AIC may not favor causal models.
The model's consistency with results is not guaranteed; as sample size increases, outcomes may change.
AIC might select complex models based on the relative magnitude and penalty terms, leading to potential overfitting.
AIC assumes all models are nested with a common subset of parameters, which may not always hold true.

Akaike Information Criterion vs Bayesian Information Criterion

The main differences and distinguishing factors between the Akaike information criterion and the Bayesian information criterion are:

Akaike Information Criterion (AIC)	Bayesian Information Criterion (BIC)
Used for unknown model selection by comparing models.	Employed with a finite set of models.
Multiplies the number of parameters by two.	Multiplies the number of parameters by the log value of the number of observations.
Developed by Hirotugu Akaike.	Developed by Gideon Schwarz; also known as the Gideon Information Criterion.

Frequently Asked Questions (FAQs)

1. What is the importance of the Akaike information criterion in factor analysis?

The Akaike Information Criterion (AIC) is crucial in factor analysis as it helps identify the most suitable model by balancing goodness of fit and simplicity. AIC considers both, making it valuable in selecting models that effectively explain observed variables.

2. Is AIC better than the P value?

Comparing AIC to p-values is like comparing apples to oranges; they serve different purposes. AIC is preferred for model selection as it balances goodness of fit and simplicity, while p-values primarily assess the significance of individual predictors.

3. Why use AIC and BIC in model selection?

AIC and Bayesian Information Criterion (BIC) aid in model selection by evaluating the trade-off between model fit and complexity. AIC allows for more flexibility by penalizing complex models less severely than BIC. Researchers choose between them based on their emphasis on model simplicity versus goodness of fit.