Table Of Contents
What Is An Adjustable Rate Mortgage Calculator?
An Adjustable-rate mortgage calculator refers to the calculators created to help users compute the periodical installment amount wherein interest rate changes after fixed intervals throughout the borrowing period.
Finance Seekers can use the adjustable rate mortgage calculators to keep a check on the provided interest rates from time to time and calculate the mortgage installment payments accordingly. This way, they would easily be able to find out and decide on fulfilling their mortgage finance needs accordingly.
Key Takeaways
- The adjustable-rate mortgage calculator assists users in estimating their periodic loan payments, considering fluctuating interest rates that change at fixed intervals throughout the borrowing period.
- Comparing variable-rate mortgages with fixed-rate mortgages reveals that banks often offer the former to mitigate interest rate risk.
- As interest rates rise, banks could end up charging customers lower interest than necessary, impacting their revenue.
- Banks might encounter increased operational costs when they've provided loans at a fixed rate. This calculator aids customers in determining new installments if interest rates change during the loan term.
About Adjustable Rate Mortgage Calculator
An adjustable rate mortgage calculator takes into consideration the interest rate assumptions. As a result, the borrowers calculating their repayment amount get the total interest to be paid over the loan period. Hence, the borrowers can easily figure out the total repayment that they would be making by the end of the loan term.
An adjustable-rate mortgage or ARM mortgage calculator could be a smart choice for those borrowers who are planning to repay the borrowing within a specific period or those who shall not be hurt financially when there is an adjustment in interest rate.
The formula for computing Adjustable Rate Mortgage is per the below steps:
Mortgage Initial Payment with Fixed-Rate
Next, we need to determine the outstanding principal balance before the rate changes.
Mortgage subsequent payments
Wherein,
- P is the loan amount
- R is the rate of interest per annum
- R’ is the rate applicable subsequently.
- N is the number of periods or frequency wherein the loan amount is to be paid.
This calculator embraces a variable rate mortgage versus only a fixed-rate mortgage. Banks generally offer these kinds of loans as the bank will not like to lock in a rate for an entire period of the loan, and if they do so, they will face interest rate risk. If the interest rate goes up in the future, the bank would still be charging less interest rate to its customers and hence will affect their revenue. Further, the cost of operating for the bank could go up, and if they have lent at a fixed rate, then that shall impact their margins and could eventually impact their revenue statement. Further, even customers prefer floating rates as, and when rates fall, they would be benefited by reduced installment amount and reduction in interest outgo. This calculator shall be used to calculate what would be the periodically new installment when there is a change in the rate of interest during the life of the loan.
How to Use?
To make sure, the results obtained through this calculator is reliable and accurate, one must ensure using it properly.
Here are a few steps that one needs to follow to calculate the Mortgage Points benefits.
- Beginning with the 1st step, one needs to enter the loan amount, which is the principal amount:
- Multiply the principal by a rate of interest fixed during the initial borrowing.
- We need to compound the same by rate until the loan period.
- We now need to discount the above result obtained in step 3 by the following:
- After entering the above formula in excel, we shall obtain installments periodically.
- In the initial period, banks would have offered the terms when the rate would change. Calculate the outstanding principal balance just before that rate change.
- Repeat steps from step 4 but this time with the new interest rate applicable and with an outstanding period.
- If there is another rate change, then step 6 and step 7 will be repeated until the last rate change is considered.
Example
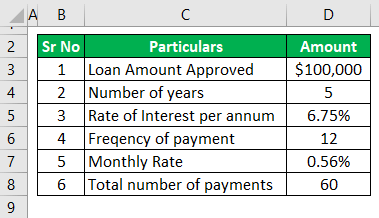
Mr. Bean has taken a very short-term mortgage loan for five years, and the term is 3/1 ARM, which means that the rate of interest will remain fixed for three years and after that rate shall change for the remaining term annually. The initial interest rate was 6.75%. It will be reset by 0.10% on every reset date. Based on the given information, you must calculate the total mortgage installment amount at each reset date, assuming the initial loan amount was $100,000 and installments are paid monthly.
Solution:
As the first step, we will first calculate the monthly installments based on the initial loan amount.
The monthly interest rate will be 6.75% / 12, which is 0.56%, and the period will be five years x 12, which is 60 months.
- = ($100,000 x 0.56% x (1 + 0.56%)^60) / ((1 + 0.56%)^60 – 1)
- = $1,968.35
Monthly Installments based on the initial loan amount are shown below:
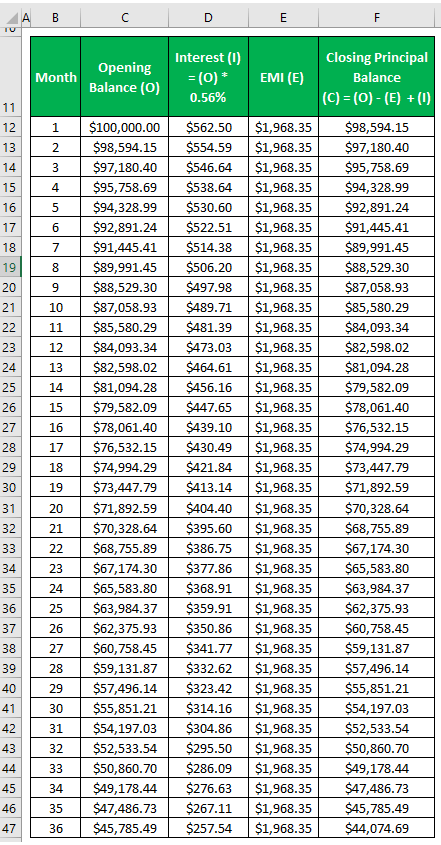
Now the rate of interest changes to 6.75% + 0.10%, which is 6.85% at the end of 3 years, and now the remaining period will be (5 x 12) – (3 x 12), that is 60 – 36, which is 24 months. Now we need to find out the principal balance at the end of year three which can be calculated below:
The monthly interest rate will be 6.85% / 12, which is 0.57%, and the outstanding principal balance is 44,074.69.
At the end of 3 years
- = ($44,074.69 x 0.57% x (1 + 0.57%)^24 ) / ((1 + 0.57%)^24 – 1)
- = $1,970.34
Monthly Installments based on the initial loan amount are shown below:
Now again rate will be changed at the end of the 4th year, which shall be 6.85% + 0.10%, which is 6.95%, and monthly it shall be 6.95% / 12, which is 0.58%, and the loan period outstanding would be ( 5 x 12 ) – ( 4 x 12 ) which is 60 – 48 which is 12 months. Now we shall find out the principal balance outstanding at the end of period 4 below:
At the end of 4 years
- = ($22,789.69 x 0.58% x (1 + 0.58%)^12 ) / ((1 + 0.58%)^12 – 1)
- = $1,971.39
Monthly Installments based on the initial loan amount are shown below:
Frequently Asked Questions (FAQs)
Are adjustable rate mortgage calculators accurate?
What is the relevance of an adjustable-rate mortgage calculator?
What are the limitations of an adjustable-rate mortgage calculator?
