Accrued Interest Formula

Accrued interest is that amount of interest, which is due for a debt or bond but not paid to the lender of the bond. Interest is accrued in the case of a bond because interest starts accumulating from the time the bond is issued. Therefore, the daily and monthly accrued interest formula plays a pivotal role in the understanding of a bond investor.

Still, the interests are generally paid as a coupon in periodical intervals like quarterly, semi-annually, or annually. So, for the period, the interest is accumulated but not paid and becomes an accrued interest. The formula of accrued interest calculation is to find out how much is the daily interest and then multiply it by the period for which it is accrued.

The accrued Interest formula calculates the interest amount earned or payable on the debt over one accounting period. Still, the same is not received or paid in the same accounting period. It is calculated by multiplying the principal amount by a rate of interest and the number of days for which debt is given or taken and then dividing it by with the number of days for which debt is given or taken, and then dividing it by the total number of days in a year.

In simpler terms, when an investor buys a bond or any interest-bearing security in the secondary market between interest payment dates, they inherit the right to receive the next interest payment. However, since interest payments are periodic, the buyer needs to reimburse the seller for the interest that has accrued since the last payment.

For instance, if a bond pays interest semi-annually and an investor purchases it a month after the last interest payment, the buyer owes the seller the interest that accrued during that one-month interim period. This accrued interest reflects the time value of money, recognizing that the lender is entitled to compensation for the delay in receiving funds.

The daily accrued interest formula is vital for accurate financial reporting and equitable transactions in the secondary market. It ensures that buyers compensate sellers fairly, reflecting the true value of the financial instrument based on the interest earned up to the settlement date. Investors and financial professionals must be aware of accrued interest when engaging in transactions to avoid discrepancies in the valuation and pricing of securities.

The accrued Interest Formula is represented as follows,

Accrued Interest Formula = Loan Amount*(Yearly Interest/365)* Period for which the Interest is Accrued

Now that we understand the basics and intricacies of the daily and monthly accrued interest formula, let us apply the theoretical knowledge to practical application through the examples below.

Example #1

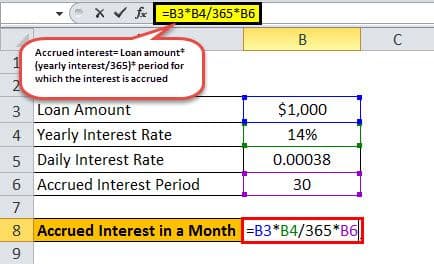
Let us understand the formula for calculating the accrued interest of a loan. Suppose the interest charged on a loan is calculated daily. Let us assume that the yearly interest rate for the loan is 14% and the amount of the loan is $1000. And the loan is payable every month. The rate of interest charged by the financial institution for the loan is monthly.

Given,

• Loan Amount=$1000
• Yearly Interest rate=14%
• The period for which the interest is accrued= 30 days

Using the above-given information, we will do the calculation of Accrued Interest as follows,

Accrued Interest formula = Loan amount*(yearly interest/365)*30

=$1,000*14%/365*30

Accrued Interest will be  -

Accrued Interest in a Month = $11.51

But the loan amount in the form of monthly installments is payable by the person who took the loan monthly. So, in this case, the accrued interest on the loan will be in the form of accrual till the point the individual does not pay the monthly installment.

Example #2

Investment in the public provident fund is an excellent practical example of understanding the accrued interest concept. Investors invest in this government scheme to save taxes under 80 c. The maximum amount to be invested in the scheme is Rs 1 50,000 a year. The yearly interest rate for the amount invested in the public provident fund is around 8%. Suppose someone has a public provident fund account and has started the account with Rs 1 50,000 as the initial investment.

The following is data for the calculation of accrued interest.

Therefore, the calculation of Accrued Interest will be as follows.

Accrued Interest will be -

Accrued Interest for Year = 12273

The interest payable on the invested amount is calculated monthly. But the interest paid by the government on the invested amount is yearly. So, in this case, the accrued interest on the investment will be in the form of accrual until the point the individual receives the yearly interest. And the interest is payable in the frequency, which is yearly, and the rate of interest is calculated based on monthly compounding.

Example #3

Investment in monthly income schemes is another excellent practical example of understanding the accrued interest concept. Suppose someone invested Rs 1,00,000 in this scheme. Suppose someone has a monthly income scheme account and has started the account with Rs 1 00,000 as the investment.

Using the above-given information, we will do the calculation of Accrued Interest as follows,

Accrued Interest formula = Loan amount*(yearly interest/365)*30

=100000*0.08/365*30

Accrued Interest will be  -

Accrued Interest Monthly = 657.53

So, the accrued interest monthly, in this case, is Rs 657, which is paid at the end of the month.

The interest payable on the invested amount is calculated daily. But the interest paid by the government on the invested amount is monthly. So, in this case, the accrued interest on the investment will be in the form of accrual until the point the individual receives the monthly interest. So, the yearly interest rate for the amount invested in the monthly income scheme is around 8%. The interest is payable in the frequency, which is monthly, and the rate of interest calculated is calculated based on daily.

The basis of the daily accrued interest formula is based on accrual-based accounting. Companies do not wait to receive receipt of cash for reporting income or expenses. Instead, income is reported whenever it is accrued. Similarly, a company that has debts in its books will have to report the amount of interest accrued for the bonds it has lent. The accrued interest is reported in the balance sheet as interest payable and comes in the current liability section of the balance sheet.

The companies also report the accrued interest in the income statement below the operating items, under the heading interest expenses. For the accrual accounting principle to be followed, companies must maintain the accrued interest portion and report the same in the financial statements during reporting 10Q and 10k.

Let us understand the differences between accrued and capitalized interest through the comparison below.

Accrued Interest

• Accrued interest is the amount of interest that accumulates on a financial instrument between the last interest payment date and the transaction's settlement date.
• It represents the earned but unpaid interest that the buyer must reimburse the seller when purchasing an interest-bearing security in the secondary market.
• Commonly associated with bonds and other fixed-income securities, accrued interest ensures a fair exchange of value, considering the periodic nature of interest payments.

Capitalized Interest

• Capitalized interest refers to the interest expenses that are added to the principal amount of a loan during a specific period, typically during construction or a similar capital project.
• It is employed to account for the cost of borrowing for the development of a long-term asset. Rather than expensing the interest immediately, it becomes part of the asset's cost and is gradually paid off over the asset's useful life.
• Common in real estate and infrastructure projects, capitalized interest allows for a more accurate reflection of the total project cost, spreading the financial burden over the asset's economic life.